题目内容
 如图所示,点M在正六边形ABCDEF的边BC、CD、DE、EF上变动,若
如图所示,点M在正六边形ABCDEF的边BC、CD、DE、EF上变动,若| AM |
| AB |
| AF |
考点:平面向量的基本定理及其意义
专题:不等式的解法及应用,平面向量及应用
分析:通过建立坐标系,写出各点的坐标及直线方程,设出动点M的坐标;
写出向量
的坐标,据已知条件中的向量等式得到α,β与x,y的关系,代入点M的可行域得α,β的取值范围,利用线性规划求出α+β的取值范围.
写出向量
| AM |
解答:
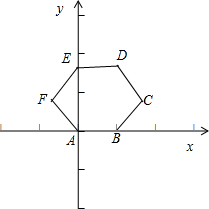 解:建立如图坐标系,不妨设AB=1,则A(0,0),B(1,0),C(
解:建立如图坐标系,不妨设AB=1,则A(0,0),B(1,0),C(
,
),D(1,
),E(0,
),F(-
,
);
则CD的方程为
x+y-2
=0(1≤x≤
,
≤y≤
),
BC的方程为
x-y-
=0(1≤x≤
,0≤y≤
),
EF 的方程为
x-y+
=0(-
≤x≤0,
≤y≤
),
DE的方程为y=
(0≤x≤1);
设
=(α,β),∵M在正六边形ABCDEF的边BC、CD、DE、EF上变动,∴
;
∵
=(1,0),
=(-
,
),
∴(α,β)=x(1,0)+y(-
,
)=(x-
y,
y);
得
,可得
,化简得
,
由线性规划的知识求得1≤x+y≤4;
∴x+y的最大值是4.
故答案为:4.
 解:建立如图坐标系,不妨设AB=1,则A(0,0),B(1,0),C(
解:建立如图坐标系,不妨设AB=1,则A(0,0),B(1,0),C(| 3 |
| 2 |
| ||
| 2 |
| 3 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
则CD的方程为
| 3 |
| 3 |
| 3 |
| 2 |
| ||
| 2 |
| 3 |
BC的方程为
| 3 |
| 3 |
| 3 |
| 2 |
| ||
| 2 |
EF 的方程为
| 3 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
DE的方程为y=
| 3 |
设
| AM |
|
∵
| AB |
| AF |
| 1 |
| 2 |
| ||
| 2 |
∴(α,β)=x(1,0)+y(-
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
得
|
|
|
由线性规划的知识求得1≤x+y≤4;
∴x+y的最大值是4.
故答案为:4.
点评:本题考查通过建立直角坐标系将问题转化为线性规划问题,通过线性规划求最大值的问题,是难题.

练习册系列答案
相关题目
已知函数y=f(x)的定义域为[2,4],则函数y=f(2x)定义域为( )
| A、[0,1] |
| B、[1,2] |
| C、[4,16] |
| D、[2,4] |
高为
的四棱锥S-ABCD的底面是边长为1的正方形,点S、A、B、C、D均在半径为1的同一球面上,底面ABCD的中心为O1,外接球的球心为O,则异面直线SO1与AB所成的最小角的余弦值为( )
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
将号码分别为1,2,3,4的四张完全相同的纸片放入一口袋中,甲从袋中摸出一个纸片,其号码为a,放回后,乙从此口袋中再摸出一纸片,其号码为b,则使不等式a-2b+1<0成立的事件发生的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
点M是曲线
+
=1(x≠±5)上任意一点,点A,B的坐标分别为(-5,0),(5,0),直线AM与直线BM的斜率之积为( )
| x2 |
| 25 |
| y2 |
| 9 |
A、-
| ||
B、
| ||
C、-
| ||
D、
|
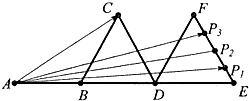 如图,△DBC,△DEF为边长为2的等边三角形,若AB=2,且P1,P2,P3是线段EF上的四等分点,则
如图,△DBC,△DEF为边长为2的等边三角形,若AB=2,且P1,P2,P3是线段EF上的四等分点,则