题目内容
9.已知$sinα=\frac{3}{5}$,$α∈(\frac{π}{2},π)$,$tan(π-β)=\frac{1}{2}$,则tan(α-β)的值为( )| A. | $-\frac{2}{11}$ | B. | $\frac{2}{11}$ | C. | $\frac{11}{2}$ | D. | $-\frac{11}{2}$ |
分析 由条件利用同角三角函数的基本关系求得tanα的值,利用诱导公式求得tanβ,再利用两角差的正切公式,求得要求式子的值.
解答 解:∵已知$sinα=\frac{3}{5}$,$α∈(\frac{π}{2},π)$,∴cosα=-$\sqrt{{1-sin}^{2}α}$=-$\frac{4}{5}$,
∴tanα=$\frac{sinα}{cosα}$=-$\frac{3}{4}$.
∵$tan(π-β)=\frac{1}{2}$=-tanβ,∴tanβ=-$\frac{1}{2}$,则tan(α-β)=$\frac{tanα-tanβ}{1+tanα•tanβ}$=-$\frac{2}{11}$,
故选:A.
点评 本题主要考查同角三角函数的基本关系,两角差的正切公式的应用,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.在复平面内,复数(1+$\sqrt{3}$i)•i对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
20.已知圆C:x2+y2-4x=0,直线l:kx-3k-y=0,则直线l与圆C的位置关系是( )
| A. | 相交 | B. | 相切 | ||
| C. | 相离 | D. | 以上三种均有可能 |
17.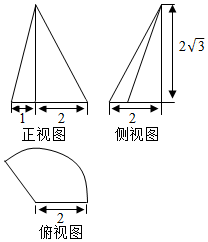 某几何体的三视图如图所示,其中俯视图为扇形,则一个质点从扇形的圆心起始,绕几何体的侧面运动一周回到起点,其最短路径为( )
某几何体的三视图如图所示,其中俯视图为扇形,则一个质点从扇形的圆心起始,绕几何体的侧面运动一周回到起点,其最短路径为( )
 某几何体的三视图如图所示,其中俯视图为扇形,则一个质点从扇形的圆心起始,绕几何体的侧面运动一周回到起点,其最短路径为( )
某几何体的三视图如图所示,其中俯视图为扇形,则一个质点从扇形的圆心起始,绕几何体的侧面运动一周回到起点,其最短路径为( )| A. | 4+$\frac{4π}{3}$ | B. | 6$\sqrt{3}$ | C. | 4+$\frac{2π}{3}$ | D. | 6 |
14.已知集合A={x|x2+2x-8≥0},B={x|1<x<5},U=R,则CU(A∪B)( )
| A. | (-4,1] | B. | [-4,1) | C. | (-2,1] | D. | [-2,1) |
1.已知点列${A_n}({{a_n},{b_n}})({n∈{N^*}})$是函数y=ax(a>0,a≠1)图象上的点,点列Bn(n,0)满足|AnBn|=|AnBn+1|,若数列{bn}中任意相邻三项能构成三角形三边,则a的取值范围是( )
| A. | $0<a<\frac{{\sqrt{5}-1}}{2}$或$a>\frac{{\sqrt{5}+1}}{2}$ | B. | $\frac{{\sqrt{5}-1}}{2}<a<1$或$1<a<\frac{{\sqrt{5}+1}}{2}$ | ||
| C. | $0<a<\frac{{\sqrt{3}-1}}{2}$或$a>\frac{{\sqrt{3}+1}}{2}$ | D. | $\frac{{\sqrt{3}-1}}{2}<a<1$或$1<a<\frac{{\sqrt{3}+1}}{2}$ |
 已知,在多面体EF-ABCD中,已知ABCD是边长为4的正方形,EF=2,EF∥AB,平面FBC⊥平面ABCD,M,N分别是AB,CD的中点.
已知,在多面体EF-ABCD中,已知ABCD是边长为4的正方形,EF=2,EF∥AB,平面FBC⊥平面ABCD,M,N分别是AB,CD的中点.