题目内容
20．已知圆C：x2+y2-4x=0，直线l：kx-3k-y=0，则直线l与圆C的位置关系是（ ）| A． | 相交 | B． | 相切 | ||
| C． | 相离 | D． | 以上三种均有可能 |
分析 由直线系方程可得直线过定点A（3，0），化圆的方程为标准方程，求出圆心坐标和半径，由两点间的距离公式可得A在圆内部，则说明直线l与圆C相交．
解答 解：由直线l：kx-3k-y=0，得k（x-3）-y=0，
∴直线l过定点A（3，0），
由圆C：x2+y2-4x=0，得（x-2）2+y2=4，
圆心坐标为C（2，0），半径r=2，
∵|AC|=$\sqrt{（3-2）^{2}+（0-0）^{2}}=1$＜2=r，
∴A在圆C内部，则直线l与圆C相交．
故选：A．
点评 本题考查了直线与圆的位置关系，考查了两点间的距离公式的运用，是基础题．
练习册系列答案
黄冈小状元解决问题天天练系列答案
三点一测快乐周计划系列答案
相关题目
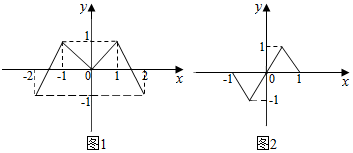已知偶函数f（x），奇函数g（x）的图象分别如图（1）、图（2）所示，方程f（g（x））=0，g（f（x））=0的实根的个数分别为a，b，则a+b=（ ）
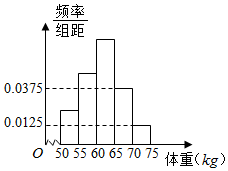如图是某学校抽取的学生体重的频率分布直方图，已知图中从左到右的前3个小组的频率依次成等差数列，第2小组的频数为10，则抽取的学生人数为40．
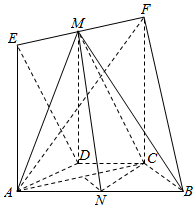如图，在几何体ABCDEF中，AB∥CD，AD=DC=CB=1，∠ABC=60°，四边形ACFE为矩形，FB=$\sqrt{10}$，M，N分别为EF，AB的中点．
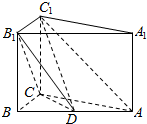已知在三棱柱ABC-A1B1C1中，AA1⊥平面ABC，AB=5，AC=AA1=4，BC=3，点D在AB上．
9．已知$sinα=\frac{3}{5}$，$α∈（\frac{π}{2}，π）$，$tan（π-β）=\frac{1}{2}$，则tan（α-β）的值为（ ）
| A． | $-\frac{2}{11}$ | B． | $\frac{2}{11}$ | C． | $\frac{11}{2}$ | D． | $-\frac{11}{2}$ |
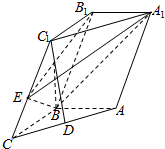如图所示，在斜三棱柱ABC-A1B1C1中，AB=BC=1，AA1=2，D是AC的中点，AB⊥平面B1C1CB，∠BCC1=60°．