题目内容
1.已知点列${A_n}({{a_n},{b_n}})({n∈{N^*}})$是函数y=ax(a>0,a≠1)图象上的点,点列Bn(n,0)满足|AnBn|=|AnBn+1|,若数列{bn}中任意相邻三项能构成三角形三边,则a的取值范围是( )| A. | $0<a<\frac{{\sqrt{5}-1}}{2}$或$a>\frac{{\sqrt{5}+1}}{2}$ | B. | $\frac{{\sqrt{5}-1}}{2}<a<1$或$1<a<\frac{{\sqrt{5}+1}}{2}$ | ||
| C. | $0<a<\frac{{\sqrt{3}-1}}{2}$或$a>\frac{{\sqrt{3}+1}}{2}$ | D. | $\frac{{\sqrt{3}-1}}{2}<a<1$或$1<a<\frac{{\sqrt{3}+1}}{2}$ |
分析 根据题意,得出an、bn的解析式,讨论a>1和0<a<1时,满足的条件,从而求出a的取值范围.
解答 解:由题意得,点Bn(n,0),An(an,bn)满足|AnBn|=|AnBn+1|,
由中点坐标公式,可得BnBn+1的中点为(n+$\frac{1}{2}$,0),
即an=n+$\frac{1}{2}$,bn=${a}^{n+\frac{1}{2}}$;
当a>1时,以bn-1,bn,bn+1为边长能构成一个三角形,
只需bn-1+bn+1>bn,
bn-1<bn<bn+1,
即${a}^{n-\frac{1}{2}}$+${a}^{n+\frac{3}{2}}$>${a}^{n+\frac{1}{2}}$,
即有1+a2<a,
解得1<a<$\frac{1+\sqrt{5}}{2}$;
同理,0<a<1时,解得$\frac{\sqrt{5}-1}{2}$<a<1;
综上,a的取值范围是1<a<$\frac{1+\sqrt{5}}{2}$或$\frac{\sqrt{5}-1}{2}$<a<1,
故选B.
点评 本题考查了指数函数的图象与性质的应用问题,也考查了数列递推公式的应用问题,考查了分类讨论思想的应用问题,是综合性题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.已知$sinα=\frac{3}{5}$,$α∈(\frac{π}{2},π)$,$tan(π-β)=\frac{1}{2}$,则tan(α-β)的值为( )
| A. | $-\frac{2}{11}$ | B. | $\frac{2}{11}$ | C. | $\frac{11}{2}$ | D. | $-\frac{11}{2}$ |
13.给定正三棱锥P-ABC,M点为底面正三角形ABC内(含边界)一点,且M到三个侧面PAB、PBC、PAC的距离依次成等差数列,则点M的轨迹为( )
| A. | 椭圆的一部分 | B. | 一条线段 | C. | 双曲线的一部分 | D. | 抛物线的一部分 |
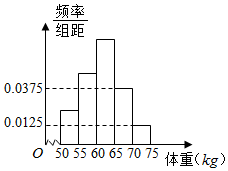 如图是某学校抽取的学生体重的频率分布直方图,已知图中从左到右的前3个小组的频率依次成等差数列,第2小组的频数为10,则抽取的学生人数为40.
如图是某学校抽取的学生体重的频率分布直方图,已知图中从左到右的前3个小组的频率依次成等差数列,第2小组的频数为10,则抽取的学生人数为40.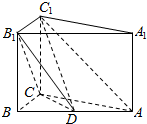 已知在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB=5,AC=AA1=4,BC=3,点D在AB上.
已知在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB=5,AC=AA1=4,BC=3,点D在AB上.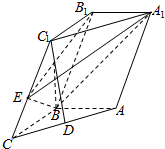 如图所示,在斜三棱柱ABC-A1B1C1中,AB=BC=1,AA1=2,D是AC的中点,AB⊥平面B1C1CB,∠BCC1=60°.
如图所示,在斜三棱柱ABC-A1B1C1中,AB=BC=1,AA1=2,D是AC的中点,AB⊥平面B1C1CB,∠BCC1=60°.