题目内容
18.小明、小红等4位同学各自申请甲、乙两所大学的自主招生考试资格,则每所大学恰有两位同学申请,且小明、小红没有申请同一所大学的可能性有4种.分析 由于小明、小红没有申请同一所大学,则组合为(AC,BD)与(AD,BC)两种形式,再分配到2个学校即可.
解答 解:设小明、小红等4位同学分别为A,B,C,D,小明、小红没有申请同一所大学,则组合为(AC,BD)与(AD,BC)
若AC选甲学校,则BD选乙学校,若AC选乙学校,则BD选甲学校,
若AD选甲学校,则BC选乙学校,若AD选乙学校,则BC选甲学校,
故共有4种方法,
故答案为:4.
点评 本题考查了简单的排列组合的问题,关键把4人分组,分组再分配,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.已知$sinα=\frac{3}{5}$,$α∈(\frac{π}{2},π)$,$tan(π-β)=\frac{1}{2}$,则tan(α-β)的值为( )
| A. | $-\frac{2}{11}$ | B. | $\frac{2}{11}$ | C. | $\frac{11}{2}$ | D. | $-\frac{11}{2}$ |
13.给定正三棱锥P-ABC,M点为底面正三角形ABC内(含边界)一点,且M到三个侧面PAB、PBC、PAC的距离依次成等差数列,则点M的轨迹为( )
| A. | 椭圆的一部分 | B. | 一条线段 | C. | 双曲线的一部分 | D. | 抛物线的一部分 |
7.定义在R上的函数f(x)满足f(x)+f(x+4)=16,当x∈(0,4]时,f(x)=x2-2x,则函数f(x)在[-4,2016]上的零点个数是( )
| A. | 504 | B. | 505 | C. | 1008 | D. | 1009 |
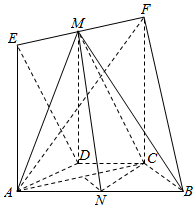 如图,在几何体ABCDEF中,AB∥CD,AD=DC=CB=1,∠ABC=60°,四边形ACFE为矩形,FB=$\sqrt{10}$,M,N分别为EF,AB的中点.
如图,在几何体ABCDEF中,AB∥CD,AD=DC=CB=1,∠ABC=60°,四边形ACFE为矩形,FB=$\sqrt{10}$,M,N分别为EF,AB的中点.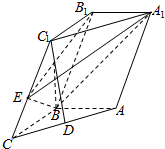 如图所示,在斜三棱柱ABC-A1B1C1中,AB=BC=1,AA1=2,D是AC的中点,AB⊥平面B1C1CB,∠BCC1=60°.
如图所示,在斜三棱柱ABC-A1B1C1中,AB=BC=1,AA1=2,D是AC的中点,AB⊥平面B1C1CB,∠BCC1=60°.