题目内容
4. 已知,在多面体EF-ABCD中,已知ABCD是边长为4的正方形,EF=2,EF∥AB,平面FBC⊥平面ABCD,M,N分别是AB,CD的中点.
已知,在多面体EF-ABCD中,已知ABCD是边长为4的正方形,EF=2,EF∥AB,平面FBC⊥平面ABCD,M,N分别是AB,CD的中点.(1)求证:平面MNE∥平面BCF;
(2)若在△BCF中,CF=$\sqrt{10}$,BC边上的高FH=3,求二面角E-AD-B的余弦值.
分析 (1)由ABCD是正方形,M、N是AB、CD中点,得MN∥BC,从而BFEM是平行四边形,由此能证明平面MNE∥平面BCF.
(2)过E作ET⊥MN,于T,延长HT交AD于K,作出二面角的平面角,结合三角形的边角关系进行求解即可.
解答 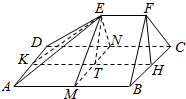 (1)证明:∵ABCD是正方形,M、N是AB、CD中点,
(1)证明:∵ABCD是正方形,M、N是AB、CD中点,
∴MN∥BC,
∵MB=2=EF,EF∥AB,
∴BFEM是平行四边形,
∴ME∥BF,
∵MN,ME?平面MNE,BC,BF?平面BCF,
∴平面MNE∥平面BCF
(2)过E作ET⊥MN,于T,
延长HT交AD于K,
则HK⊥AD,连接EK,
则EK⊥AD,
即∠EKT是二面角E-AD-B的平面角,
∵BC边上的高FH=3,
∴EN=FH=3,KT=2,
则EK=$\sqrt{{3}^{2}+{2}^{2}}=\sqrt{9+4}$=$\sqrt{13}$,
则cos∠EKT=$\frac{KT}{EK}$=$\frac{2}{\sqrt{13}}=\frac{2\sqrt{13}}{13}$.
点评 本题考查平面与平面平行的证明,考查二面角的求法,根据条件作出二面角的平面角是解决本题的关键.解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
9.已知$sinα=\frac{3}{5}$,$α∈(\frac{π}{2},π)$,$tan(π-β)=\frac{1}{2}$,则tan(α-β)的值为( )
| A. | $-\frac{2}{11}$ | B. | $\frac{2}{11}$ | C. | $\frac{11}{2}$ | D. | $-\frac{11}{2}$ |
13.给定正三棱锥P-ABC,M点为底面正三角形ABC内(含边界)一点,且M到三个侧面PAB、PBC、PAC的距离依次成等差数列,则点M的轨迹为( )
| A. | 椭圆的一部分 | B. | 一条线段 | C. | 双曲线的一部分 | D. | 抛物线的一部分 |
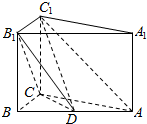 已知在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB=5,AC=AA1=4,BC=3,点D在AB上.
已知在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB=5,AC=AA1=4,BC=3,点D在AB上.