题目内容
17.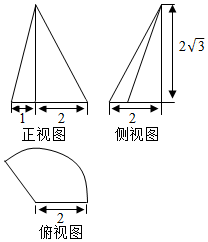 某几何体的三视图如图所示,其中俯视图为扇形,则一个质点从扇形的圆心起始,绕几何体的侧面运动一周回到起点,其最短路径为( )
某几何体的三视图如图所示,其中俯视图为扇形,则一个质点从扇形的圆心起始,绕几何体的侧面运动一周回到起点,其最短路径为( )| A. | 4+$\frac{4π}{3}$ | B. | 6$\sqrt{3}$ | C. | 4+$\frac{2π}{3}$ | D. | 6 |
分析 作出几何体侧面展开图,将问题转化为平面上的最短问题解决.
解答  解:由三视图可知几何体为圆锥的一部分,圆锥的底面半径为2,几何体底面圆心角为120°,
解:由三视图可知几何体为圆锥的一部分,圆锥的底面半径为2,几何体底面圆心角为120°,
∴几何体底面弧长为$\frac{1}{3}×2π×2$=$\frac{4π}{3}$.
圆锥高为2$\sqrt{3}$.∴圆锥的母线长为$\sqrt{{2}^{2}+(2\sqrt{3})^{2}}=4$.
作出几何体的侧面展开图如图所示:
其中,AB=AB′=2$\sqrt{3}$,AB⊥BC,AB′⊥B′D,B′D=BC=2,
AC=AD=4,$\widehat{CD}=\frac{4π}{3}$.
∴∠BAC=∠B′AD=30°,∠CAD=$\frac{\widehat{CD}}{AC}=\frac{π}{3}=60°$.
∴∠BAB′=120°.
∴BB′=$\sqrt{A{B}^{2}+AB{′}^{2}-2AB•AB′cos120°}$=6.
故选D.
点评 本题考查了圆锥的侧面展开图,曲面上最短路径问题,作出侧面展开图是解题关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
7.设集合S={1,2,…,2016},若X是S的子集,把X中所有元素之和称为X的“容量”,(规定空集容量为0),若X的容量为奇(偶)数,则称X为S的奇(偶)子集,记S的奇子集个数为m,偶子集个数为n,则m,n之间的关系为( )
| A. | m=n | B. | m>n | C. | m<n | D. | 无法确定 |
9.已知$sinα=\frac{3}{5}$,$α∈(\frac{π}{2},π)$,$tan(π-β)=\frac{1}{2}$,则tan(α-β)的值为( )
| A. | $-\frac{2}{11}$ | B. | $\frac{2}{11}$ | C. | $\frac{11}{2}$ | D. | $-\frac{11}{2}$ |
7.定义在R上的函数f(x)满足f(x)+f(x+4)=16,当x∈(0,4]时,f(x)=x2-2x,则函数f(x)在[-4,2016]上的零点个数是( )
| A. | 504 | B. | 505 | C. | 1008 | D. | 1009 |
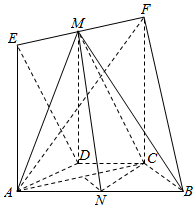 如图,在几何体ABCDEF中,AB∥CD,AD=DC=CB=1,∠ABC=60°,四边形ACFE为矩形,FB=$\sqrt{10}$,M,N分别为EF,AB的中点.
如图,在几何体ABCDEF中,AB∥CD,AD=DC=CB=1,∠ABC=60°,四边形ACFE为矩形,FB=$\sqrt{10}$,M,N分别为EF,AB的中点.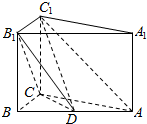 已知在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB=5,AC=AA1=4,BC=3,点D在AB上.
已知在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB=5,AC=AA1=4,BC=3,点D在AB上.