题目内容
19.在复平面内,复数(1+$\sqrt{3}$i)•i对应的点位于( )| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
分析 写出复数的对应点的坐标,判断即可.
解答 解:复数(1+$\sqrt{3}$i)•i=-$\sqrt{3}$+i.对应点为(-$\sqrt{3}$,1)在第二象限.
故选:B.
点评 本题考查复数的几何意义,考查计算能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7.设集合S={1,2,…,2016},若X是S的子集,把X中所有元素之和称为X的“容量”,(规定空集容量为0),若X的容量为奇(偶)数,则称X为S的奇(偶)子集,记S的奇子集个数为m,偶子集个数为n,则m,n之间的关系为( )
| A. | m=n | B. | m>n | C. | m<n | D. | 无法确定 |
4.阅读如图所示的程序框图,运行相应的程序,若判断框内是n≤6,则输出的S为( )
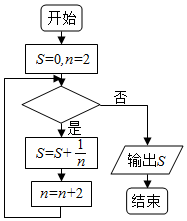

| A. | $\frac{3}{4}$ | B. | $\frac{25}{24}$ | C. | $\frac{11}{12}$ | D. | $\frac{5}{6}$ |
9.已知$sinα=\frac{3}{5}$,$α∈(\frac{π}{2},π)$,$tan(π-β)=\frac{1}{2}$,则tan(α-β)的值为( )
| A. | $-\frac{2}{11}$ | B. | $\frac{2}{11}$ | C. | $\frac{11}{2}$ | D. | $-\frac{11}{2}$ |
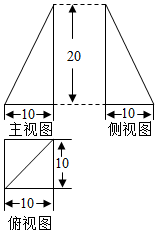 董师傅用铁皮制作一封闭的工件,且三视图如图所示(单位:cm),图中水平线与竖直线垂直),则制作该工件用去的铁皮的面积为(制作过程铁皮的损耗忽略不计)(100(3+$\sqrt{5}$)cm2.
董师傅用铁皮制作一封闭的工件,且三视图如图所示(单位:cm),图中水平线与竖直线垂直),则制作该工件用去的铁皮的面积为(制作过程铁皮的损耗忽略不计)(100(3+$\sqrt{5}$)cm2.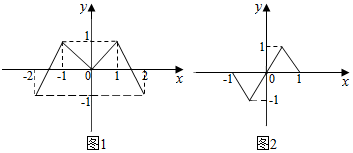 已知偶函数f(x),奇函数g(x)的图象分别如图(1)、图(2)所示,方程f(g(x))=0,g(f(x))=0的实根的个数分别为a,b,则a+b=( )
已知偶函数f(x),奇函数g(x)的图象分别如图(1)、图(2)所示,方程f(g(x))=0,g(f(x))=0的实根的个数分别为a,b,则a+b=( )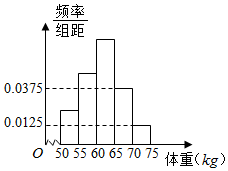 如图是某学校抽取的学生体重的频率分布直方图,已知图中从左到右的前3个小组的频率依次成等差数列,第2小组的频数为10,则抽取的学生人数为40.
如图是某学校抽取的学生体重的频率分布直方图,已知图中从左到右的前3个小组的频率依次成等差数列,第2小组的频数为10,则抽取的学生人数为40.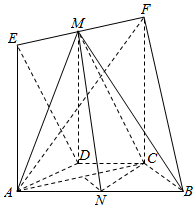 如图,在几何体ABCDEF中,AB∥CD,AD=DC=CB=1,∠ABC=60°,四边形ACFE为矩形,FB=$\sqrt{10}$,M,N分别为EF,AB的中点.
如图,在几何体ABCDEF中,AB∥CD,AD=DC=CB=1,∠ABC=60°,四边形ACFE为矩形,FB=$\sqrt{10}$,M,N分别为EF,AB的中点.