题目内容
14.已知集合A={x|x2+2x-8≥0},B={x|1<x<5},U=R,则CU(A∪B)( )| A. | (-4,1] | B. | [-4,1) | C. | (-2,1] | D. | [-2,1) |
分析 化简集合A,求出A∪B,再求CU(A∪B)即可.
解答 解:∵集合A={x|x2+2x-8≥0}={x|x≤-4或x≥2},
B={x|1<x<5},U=R,
∴A∪B={x|x≤-4或x<1},
∴CU(A∪B)={x|-4<x≤1}=(-4,1].
故选:A.
点评 本题考查了集合的化简与运算问题,是基础题目.

练习册系列答案
相关题目
4.阅读如图所示的程序框图,运行相应的程序,若判断框内是n≤6,则输出的S为( )
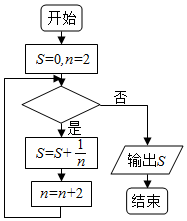

| A. | $\frac{3}{4}$ | B. | $\frac{25}{24}$ | C. | $\frac{11}{12}$ | D. | $\frac{5}{6}$ |
9.已知$sinα=\frac{3}{5}$,$α∈(\frac{π}{2},π)$,$tan(π-β)=\frac{1}{2}$,则tan(α-β)的值为( )
| A. | $-\frac{2}{11}$ | B. | $\frac{2}{11}$ | C. | $\frac{11}{2}$ | D. | $-\frac{11}{2}$ |
19.函数f(x)=sin2x和函数g(x)的部分图象如图所示,则函数g(x)的解析式可以是( )

| A. | g(x)=sin(2x-$\frac{π}{3}}$) | B. | g(x)=sin(2x+$\frac{2π}{3}}$) | C. | g(x)=cos(2x+$\frac{5π}{6}}$) | D. | g(x)=cos(2x-$\frac{π}{6}}$) |
4.直线x=1,x=2,y=0及曲线y=x3围成的平面图形的面积为( )
| A. | $\sum_{i=1}^{n}$$\frac{1}{n}$(1+$\frac{i}{n}$)3 | B. | ${∫}_{1}^{2}$x3dx | C. | ${∫}_{2}^{1}$x3dx | D. | 1 |