题目内容
17．设函数f（x）=$\left\{\begin{array}{l}{-{x}^{2}+2x+a+1，x＜2}\\{x+{a}^{2}，x≥2}\end{array}\right.$的值域为R，则实数a的取值范围为[0，1]．分析 根据分段函数的表达式，分别求出每一段上函数的取值范围进行求解即可．
解答 
解：当x≥2时，f（x）=x+a2≥2+a2，
当x＜2时，f（x）=-x2+2x+a+1=-（x-1）2+a+2≤a+2，
∵f（x）=$\left\{\begin{array}{l}{-{x}^{2}+2x+a+1，x＜2}\\{x+{a}^{2}，x≥2}\end{array}\right.$的值域为R，
∴2+a2≤a+2，
即a2-a≤0，
解得0≤a≤1，
故答案为：[0，1]
点评 本题主要考查分段函数的应用，根据函数值域的关系建立不等式关系是解决本题的关键．
练习册系列答案
口算题天天练系列答案
相关题目
8．设α，β是两个不同的平面，m，n是两条不同的直线，下列命题中正确的是（ ）
| A． | 若α⊥β，m?α，则m⊥β | B． | 若α⊥β，m⊥α，则m∥β | ||
| C． | 若m∥α，α∩β=n，则m∥n | D． | 若m∥α，m∥β，α∩β=n，则m∥n |
5．下列函数中，既是奇函数又存在零点的是（ ）
| A． | $y=cos（{\frac{π}{2}-x}）$ | B． | $y=sin（{\frac{π}{2}-x}）$ | C． | y=lnx | D． | $y=x+\frac{1}{x}$ |
6．某四面体的三视图如图所示，该四面体外接球的表面积为（ ）
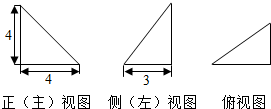
| A． | 41π | B． | $\frac{41π}{2}$ | C． | 48π | D． | 24π |