题目内容
7.已知xy-(x+y)=1(x,y为正实数),则x•y的最小值为$3+2\sqrt{2}$.分析 利用基本不等式的性质与一元二次不等式的解法即可得出.
解答 解:∵x,y为正实数,
∴xy=(x+y)+1≥2$\sqrt{xy}$+1,当且仅当x=y时取等号.
化为$(\sqrt{xy})^{2}$-2$\sqrt{xy}$-1≥0,
解得$\sqrt{xy}$≥1+$\sqrt{2}$,
∴xy≥3+2$\sqrt{2}$.
故答案为:3+2$\sqrt{2}$.
点评 本题考查了基本不等式的性质与一元二次不等式的解法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
15.如图程序执行完的结果是( )


| A. | 5,-1 | B. | 4,-6 | C. | 1,-3 | D. | 无正确答案 |
19.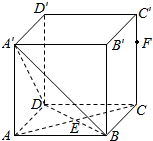 如图,正方体ABCD-A′B′C′D′中,$\overrightarrow{BD}=2\overrightarrow{BE}$.设点F在线段CC'上,直线EF与平面A'BD所成的角为α,则sinα的取值范围是( )
如图,正方体ABCD-A′B′C′D′中,$\overrightarrow{BD}=2\overrightarrow{BE}$.设点F在线段CC'上,直线EF与平面A'BD所成的角为α,则sinα的取值范围是( )
 如图,正方体ABCD-A′B′C′D′中,$\overrightarrow{BD}=2\overrightarrow{BE}$.设点F在线段CC'上,直线EF与平面A'BD所成的角为α,则sinα的取值范围是( )
如图,正方体ABCD-A′B′C′D′中,$\overrightarrow{BD}=2\overrightarrow{BE}$.设点F在线段CC'上,直线EF与平面A'BD所成的角为α,则sinα的取值范围是( )| A. | $[\frac{{\sqrt{3}}}{3},1]$ | B. | $[\frac{{2\sqrt{2}}}{3},1]$ | C. | $[\frac{{\sqrt{6}}}{3},\frac{{2\sqrt{2}}}{3}]$ | D. | $[\frac{{\sqrt{6}}}{3},1]$ |
 如图,在正三棱柱ABC-A1B1C1(侧棱垂直于底面,且底面是正三角形)中,AC=CC1=6,M是棱CC1上一点.
如图,在正三棱柱ABC-A1B1C1(侧棱垂直于底面,且底面是正三角形)中,AC=CC1=6,M是棱CC1上一点.