题目内容
8.设α,β是两个不同的平面,m,n是两条不同的直线,下列命题中正确的是( )| A. | 若α⊥β,m?α,则m⊥β | B. | 若α⊥β,m⊥α,则m∥β | ||
| C. | 若m∥α,α∩β=n,则m∥n | D. | 若m∥α,m∥β,α∩β=n,则m∥n |
分析 在A中,m与β相交、平行或m?β;在B中,m∥β或m?β;在C中,m与n平行或异面;在D中,由直线与平面平行的性质定理得m∥n.
解答 解:由α,β是两个不同的平面,m,n是两条不同的直线,知:
在A中,若α⊥β,m?α,则m与β相交、平行或m?β,故A错误;
在B中,若α⊥β,m⊥α,则m∥β或m?β,故B错误;
在C中,若m∥α,α∩β=n,则m与n平行或异面,故C错误;
在D中,若m∥α,m∥β,α∩β=n,则由直线与平面平行的性质定理得m∥n,故D正确.
故选:D.
点评 本题考查命题真假的判断,是中档题,解题时要认真审题,注意空间中线线、线面、面面间的位置关系的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19.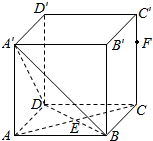 如图,正方体ABCD-A′B′C′D′中,$\overrightarrow{BD}=2\overrightarrow{BE}$.设点F在线段CC'上,直线EF与平面A'BD所成的角为α,则sinα的取值范围是( )
如图,正方体ABCD-A′B′C′D′中,$\overrightarrow{BD}=2\overrightarrow{BE}$.设点F在线段CC'上,直线EF与平面A'BD所成的角为α,则sinα的取值范围是( )
 如图,正方体ABCD-A′B′C′D′中,$\overrightarrow{BD}=2\overrightarrow{BE}$.设点F在线段CC'上,直线EF与平面A'BD所成的角为α,则sinα的取值范围是( )
如图,正方体ABCD-A′B′C′D′中,$\overrightarrow{BD}=2\overrightarrow{BE}$.设点F在线段CC'上,直线EF与平面A'BD所成的角为α,则sinα的取值范围是( )| A. | $[\frac{{\sqrt{3}}}{3},1]$ | B. | $[\frac{{2\sqrt{2}}}{3},1]$ | C. | $[\frac{{\sqrt{6}}}{3},\frac{{2\sqrt{2}}}{3}]$ | D. | $[\frac{{\sqrt{6}}}{3},1]$ |
3.设直线x-$\sqrt{3}$y+3=0与圆心为O的圆x2+y2=3交于A,B两点,则直线AO与BO的倾斜角之和为( )
| A. | $\frac{7π}{6}$ | B. | $\frac{5π}{4}$ | C. | $\frac{4π}{3}$ | D. | $\frac{5π}{3}$ |
13.在△ABC中,角A,B,C的对边分别为a,b,c,若c=2,b=2$\sqrt{3}$,C=30°,则角B等于(
| A. | 30° | B. | 60° | C. | 30°或60° | D. | 60°或120° |
20.实数x,y满足x≥1,y≥1,且(logax)2+(logay)2=loga(ax2)+loga(ay2)(0<a<1),则loga(xy)的取值范围是( )
| A. | [2-2$\sqrt{2}$,2+2$\sqrt{2}$] | B. | [2-2$\sqrt{2}$,1-$\sqrt{3}$] | ||
| C. | [1+$\sqrt{3}$,2+2$\sqrt{2}$] | D. | [2-2$\sqrt{2}$,1-$\sqrt{3}$]∪[1+$\sqrt{3}$,2+2$\sqrt{2}$] |
 如图,在正三棱柱ABC-A1B1C1(侧棱垂直于底面,且底面是正三角形)中,AC=CC1=6,M是棱CC1上一点.
如图,在正三棱柱ABC-A1B1C1(侧棱垂直于底面,且底面是正三角形)中,AC=CC1=6,M是棱CC1上一点. 如图,直三棱柱ABC-A1B1C1中,E,F,G分别为B1C1,CC1,AC的中点.
如图,直三棱柱ABC-A1B1C1中,E,F,G分别为B1C1,CC1,AC的中点.