题目内容
9．若关于x的不等式ax2-2x-2-a＜0的解集中仅有4个整数解，则实数a的取值范围为[$\frac{2}{3}$，1）．分析 由题意得到a＞0，解出二次不等式，根据解的区间端点范围可得a的范围．
解答 解：关于x的不等式ax2-2x-2-a＜0的解集中仅有4个整数解，
∴$\left\{\begin{array}{l}{a＞0}\\{△=4+4a（a+2）＞0}\end{array}\right.$，
解得a＞0，
解不等式得-1＜x＜$\frac{a+2}{a}$，
要使不等式的解集中仅有4个整数解，
∴3＜$\frac{a+2}{a}$≤4，
解得$\frac{2}{3}$≤a＜1，
故答案为：[$\frac{2}{3}$，1）．
点评 本题考查一元二次不等式的解法，考查学生分析解决问题的能力，属中档题．
练习册系列答案
相关题目
19．
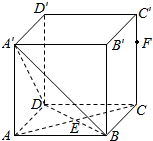如图，正方体ABCD-A′B′C′D′中，$\overrightarrow{BD}=2\overrightarrow{BE}$．设点F在线段CC'上，直线EF与平面A'BD所成的角为α，则sinα的取值范围是（ ）
如图，正方体ABCD-A′B′C′D′中，$\overrightarrow{BD}=2\overrightarrow{BE}$．设点F在线段CC'上，直线EF与平面A'BD所成的角为α，则sinα的取值范围是（ ）| A． | $[\frac{{\sqrt{3}}}{3}，1]$ | B． | $[\frac{{2\sqrt{2}}}{3}，1]$ | C． | $[\frac{{\sqrt{6}}}{3}，\frac{{2\sqrt{2}}}{3}]$ | D． | $[\frac{{\sqrt{6}}}{3}，1]$ |
20．实数x，y满足x≥1，y≥1，且（logax）2+（logay）2=loga（ax2）+loga（ay2）（0＜a＜1），则loga（xy）的取值范围是（ ）
| A． | [2-2$\sqrt{2}$，2+2$\sqrt{2}$] | B． | [2-2$\sqrt{2}$，1-$\sqrt{3}$] | ||
| C． | [1+$\sqrt{3}$，2+2$\sqrt{2}$] | D． | [2-2$\sqrt{2}$，1-$\sqrt{3}$]∪[1+$\sqrt{3}$，2+2$\sqrt{2}$] |
如图，直三棱柱ABC-A1B1C1中，E，F，G分别为B1C1，CC1，AC的中点．