题目内容
对于两个定义域相同的函数f(x),g(x),若存在实数m,n使h(x)=mf(x)+ng(x),则称函数h(x)是由“基函数f(x),g(x)”生成的.
(1)若h(x)=2x2+3x-1由函数f(x)=x2+ax,g(x)=x+b(a,b∈R,ab≠0)生成,求a+2b的取值范围;
(2)利用“基函数f(x)=xex+x2,g(x)=x2”生成一个函数h(x),使之满足下列条件:
①m+n=0;②有最小值-
,试探究是否存在实数a,使得对任意的x1,x2∈(a,+∞),当x1<x2时恒有
>
成立,若存在,求a的取值范围;若不存在,请说明理由.
(1)若h(x)=2x2+3x-1由函数f(x)=x2+ax,g(x)=x+b(a,b∈R,ab≠0)生成,求a+2b的取值范围;
(2)利用“基函数f(x)=xex+x2,g(x)=x2”生成一个函数h(x),使之满足下列条件:
①m+n=0;②有最小值-
| 1 |
| e |
| h(x2)-h(a) |
| x2-a |
| h(x1)-h(a) |
| x1-a |
考点:函数恒成立问题
专题:导数的综合应用
分析:(1)设h(x)=2x2+3x-1=m(x2+ax)+n(x+b),展开后整理,由系数相等把a,b用n表示,然后结合n的范围求得a+2b的取值范围;
(2)设h(x)=mxex+mx2-mx2=mxex,由题意求出满足条件的m值,得到函数解析式,把对任意的x1,x2∈(a,+∞),当x1<x2时恒有
>
成立转化为函数h(x)的导函数在(a,+∞)上的导函数为增函数求解.
(2)设h(x)=mxex+mx2-mx2=mxex,由题意求出满足条件的m值,得到函数解析式,把对任意的x1,x2∈(a,+∞),当x1<x2时恒有
| h(x2)-h(a) |
| x2-a |
| h(x1)-h(a) |
| x1-a |
解答:
解:(1)设h(x)=2x2+3x-1=m(x2+ax)+n(x+b)=mx2+(am+n)x+nb,
∴
,得
.
∴a+2b=
-
=
-
-
.
由ab≠0知,n≠3,
∴a+2b∈(-∞,-
)∪(
,+∞);
(2)设h(x)=mxex+mx2-mx2=mxex,
h′(x)=mex+mxex=m(x+1)ex,
函数h(x)有最小值-
,即当x=-1时函数h(x)有最小值为-me-1=-
,即m=1.
∴h(x)=xex.
若存在实数a,使得对任意的x1,x2∈(a,+∞),当x1<x2时恒有
>
成立,
说明函数h(x)=xex在(a,+∞)上的导函数为增函数,
由h(x)=xex,得h′(x)=ex+xex=(x+1)ex,
令t(x)=(x+1)ex,
则t′(x)=(x+2)ex,由(x+2)ex>0,得x>-2.
∴满足条件的a的取值范围是(-2,+∞).
∴
|
|
∴a+2b=
| 3-n |
| 2 |
| 2 |
| n |
| 3 |
| 2 |
| n |
| 2 |
| 2 |
| n |
由ab≠0知,n≠3,
∴a+2b∈(-∞,-
| 1 |
| 2 |
| 7 |
| 2 |
(2)设h(x)=mxex+mx2-mx2=mxex,
h′(x)=mex+mxex=m(x+1)ex,
函数h(x)有最小值-
| 1 |
| e |
| 1 |
| e |
∴h(x)=xex.
若存在实数a,使得对任意的x1,x2∈(a,+∞),当x1<x2时恒有
| h(x2)-h(a) |
| x2-a |
| h(x1)-h(a) |
| x1-a |
说明函数h(x)=xex在(a,+∞)上的导函数为增函数,
由h(x)=xex,得h′(x)=ex+xex=(x+1)ex,
令t(x)=(x+1)ex,
则t′(x)=(x+2)ex,由(x+2)ex>0,得x>-2.
∴满足条件的a的取值范围是(-2,+∞).
点评:本题考查了函数恒成立问题,考查了数学转化思想方法,训练了利用导数求函数的最值,关键是对题意的理解与合理转化,是压轴题.

练习册系列答案
相关题目
已知函数f(x)=
(x∈R),则下列结论中不正确的是( )
| x |
| 1+|x| |
| A、对任意x∈R,等式f(-x)+f(x)=0恒成立 |
| B、函数f(x)的值域为(-1,1) |
| C、对任意x1,x2∈R,若x1≠x2,则一定有f(x1)≠f(x2) |
| D、方程f(x)-x=0则R上有三个根 |
已知某几何本的直观图和三视图如图,则下列判定正确的是( )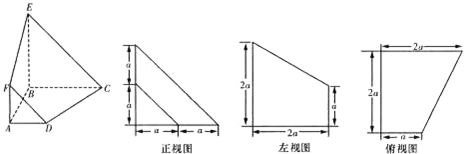

| A、DF∥CE,且BA、CD、EF的延长线不交于同一点 |
| B、DF∥CE,且BA、CD、EF的延长线交于一点 |
| C、DF与CE是异面直线 |
| D、DF与CE相交于一点 |
 如图,在四棱锥P-ABCD中,PA=PB=PD=AB=BC=CD=DA=DB=2,E为的PC中点.
如图,在四棱锥P-ABCD中,PA=PB=PD=AB=BC=CD=DA=DB=2,E为的PC中点.