题目内容
已知椭圆
+
=1,经过焦点F1做一直线交椭圆于A、B两点,求l的斜率k=-1时,求弦长.
| y2 |
| 25 |
| x2 |
| 16 |
考点:直线与圆锥曲线的关系
专题:圆锥曲线的定义、性质与方程
分析:求出椭圆的焦点F1(0,3),根据点斜率式方程设AB:y-3=-(x-0),与椭圆方程消去y得
+
=1,利用根与系数的关系算出A、B的横坐标满足|x1-x2|,最后根据弦长公式即可算出弦AB的长.
| y2 |
| 25 |
| x2 |
| 16 |
解答:
解:∵椭圆方程为
+
=1,
∴焦点分别为F1(0,3),F2(0,-3),
∵直线AB过焦点F1直线的斜率为-1.
∴直线AB的方程为y-3=-(x-0),即y=3-x
将AB方程与椭圆方程消去y,得41x2-96x-256=0
设A(x1,y1),B(x2,y2),可得
x1+x2=
,x1x2=-
.
∴|x1-x2|=
=
因此,|AB|=
•|x1-x2|=
•
=
.
故答案为:2
| y2 |
| 25 |
| x2 |
| 16 |
∴焦点分别为F1(0,3),F2(0,-3),
∵直线AB过焦点F1直线的斜率为-1.
∴直线AB的方程为y-3=-(x-0),即y=3-x
将AB方程与椭圆方程消去y,得41x2-96x-256=0
设A(x1,y1),B(x2,y2),可得
x1+x2=
| 96 |
| 41 |
| 256 |
| 41 |
∴|x1-x2|=
| (x1+x2)2-4x1x2 |
160
| ||
| 41 |
因此,|AB|=
| 1+k2 |
| 1+(-1)2 |
160
| ||
| 41 |
| 320 |
| 41 |
故答案为:2
点评:本题给出椭圆方程,求解经过焦点且斜率为-1,直线的弦AB,求弦长.着重考查了椭圆的标准方程与简单几何性质、直线与椭圆的位置关系等知识,属于中档题.

练习册系列答案
相关题目
已知函数f(x)=ex-1,g(x)=-x2+4x-3,若有f(a)=g(b),则a的取值范围为( )
A、[2-
| ||||
| B、(-∞,ln2] | ||||
C、(2-
| ||||
| D、(ln2,+∞) |
函数f(x)=
是增函数,则实数c的取值范围是( )
|
| A、[-1,+∞) |
| B、(-1,+∞) |
| C、(-∞,-1) |
| D、(-∞,-1] |
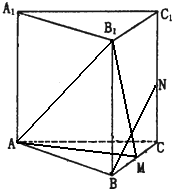 如图所示,正三棱柱ABC-A1B1C1中,各棱长均为4,M、N分别是BC、CC1的中点.
如图所示,正三棱柱ABC-A1B1C1中,各棱长均为4,M、N分别是BC、CC1的中点.