题目内容
 如图,在四棱锥P-ABCD中,PA=PB=PD=AB=BC=CD=DA=DB=2,E为的PC中点.
如图,在四棱锥P-ABCD中,PA=PB=PD=AB=BC=CD=DA=DB=2,E为的PC中点.(1)求证:PA∥平面BDE;
(2)求证:平面PBC⊥平面PDC.
考点:平面与平面垂直的判定,直线与平面平行的判定
专题:空间位置关系与距离
分析:(1)连接AC交BD于O,连接EO,PO,证明PA∥EO,利用直线与平面平行的判定定理证明PA∥平面BDE.
(2)在△PAC中,推出∠APC=90°,求出PC,然后证明BE⊥DE,BE⊥PC,得到BE⊥面PDC,利用平面与平面垂直的判定定理证明平面PBC⊥平面PDC.
(2)在△PAC中,推出∠APC=90°,求出PC,然后证明BE⊥DE,BE⊥PC,得到BE⊥面PDC,利用平面与平面垂直的判定定理证明平面PBC⊥平面PDC.
解答:
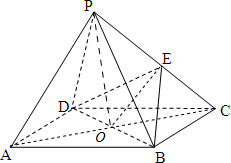 证明(1)连接AC交BD于O,连接EO,PO
证明(1)连接AC交BD于O,连接EO,PO
∵四边形ABCD是菱形,∴O是AC中点,…(2分)
又E为PC中点.∴PA∥EO…(4分)
又EO?面BDE,PA?面BDE∴PA∥平面BDE…(7分)
(2)在△PAC中,易得AO=CO=PO=
∴∠APC=90°,∴PC=2
…(9分)
∴在△PDC中可求得DE=
,同理在△PBC中可求得BE=
∴在△BDE中可得∠BED=90°,即BE⊥DE…(11分)
又PB=BC,E为PC中点,∴BE⊥PC…(12分)
BE⊥面PDC,又BE?面PBC
∴平面PBC⊥平面PDC…(14分)
 证明(1)连接AC交BD于O,连接EO,PO
证明(1)连接AC交BD于O,连接EO,PO∵四边形ABCD是菱形,∴O是AC中点,…(2分)
又E为PC中点.∴PA∥EO…(4分)
又EO?面BDE,PA?面BDE∴PA∥平面BDE…(7分)
(2)在△PAC中,易得AO=CO=PO=
| 3 |
∴∠APC=90°,∴PC=2
| 2 |
∴在△PDC中可求得DE=
| 2 |
| 2 |
∴在△BDE中可得∠BED=90°,即BE⊥DE…(11分)
又PB=BC,E为PC中点,∴BE⊥PC…(12分)
BE⊥面PDC,又BE?面PBC
∴平面PBC⊥平面PDC…(14分)
点评:本题考查直线与平面平行的判定定理以及平面与平面垂直的判定定理的应用,考查空间想象能力以及逻辑推理能力.

练习册系列答案
相关题目
已知向量
=(3,4),
=(6,-3),
=(5-x,-3-y)(其中O为坐标原点).
(1)若A,B,C三点共线,求y关于x的表达式;
(2)若△ABC是以∠B为直角的等腰三角形,求x,y的值.
| OA |
| OB |
| OC |
(1)若A,B,C三点共线,求y关于x的表达式;
(2)若△ABC是以∠B为直角的等腰三角形,求x,y的值.
已知函数f(x)=ex-1,g(x)=-x2+4x-3,若有f(a)=g(b),则a的取值范围为( )
A、[2-
| ||||
| B、(-∞,ln2] | ||||
C、(2-
| ||||
| D、(ln2,+∞) |
设集合A={x|x=n+(n2-1)i,n∈R,i为虚数单位),若A⊆R(R为实数集)则n的值为( )
| A、1 | B、-1 | C、±1 | D、0 |
