题目内容

在△ABC中，cosA=
1
3
，则sin（A+
π
4
）=
 
．
考点：两角和与差的正弦函数
专题：三角函数的求值
分析：由题意可得sinA，代入两角和的正弦函数公式可得．
解答： 解：∵在△ABC中，cosA=
1
3
，
∴sinA=
1-cos2A
=
2
2
3
，
∴sin（A+
π
4
）=
2
2
sinA+
2
2
cosA
=
2
2
×
2
2
3
+
2
2
×
1
3
=
4+
2
6

故答案为：
4+
2
6
点评：本题考查两角和与差的正弦函数，属基础题．
练习册系列答案
相关题目
抛掷一枚质地不均匀的骰子，出现向上点数为1，2，3，4，5，6的概率依次记为p1，p2，p3，p4，p5，p6，经统计发现，数列{pn}恰好构成等差数列，且p4是p1的3倍．
（Ⅰ）求数列{pn}的通项公式．
（Ⅱ）甲、乙两人用这枚骰子玩游戏，并规定：掷一次骰子后，若向上点数为奇数，则甲获胜，否则已获胜，请问这样的规则对甲、乙二人是否公平？请说明理由；
（Ⅲ）甲、乙、丙三人用这枚骰子玩游戏，根据掷一次后向上的点数决定胜出者，并制定了公平的游戏方案，试在下面的表格中列举出两种可能的方案（不必证明）．
方案序号 甲胜出对应点数 乙胜出对应点数 丙胜出对应点数
 ①      
 ②      
已知实数x、y、z满足2x2+3y2+6z2=a（a＞0），且x+y+z的最大值是1，求a的值．
已知等差数列{an}的首项al=1，公差d＞0，且第二项、第五项、第十四项分别是一个等比数列的第二项、第三项、第四项，
（1）求数列{an}的通项公式：
（2）设bn=
1
n(an+5)
（n∈N*），Sn=b1+b2+…+bn是否存在最大的整数t，使得对任意的n均有Sn＞
t
36
总成立？若存在，求出t：若不存在，请说明理由．
在平面上有如下命题：“O为直线AB外的一点，则点P在直线AB上的充要条件是：存在实数x，y满足
OP
=x
OA
+y
OB
，且x+y=1”，我们把它称为平面中三点共线定理，请尝试类比此命题，给出空间中四点共面定理，应描述为：
 
．
若实数x，y满足不等式组
3x-y≤3
x+y≥1
x-y≥-1
，则z=2x-y+1的最小值是
 
．
已知直线l的参数方程为：
x=-2+tcosα
y=tsinα
（t为参数），以坐标原点O为极点，x轴的正半轴为极轴建立极坐标系，曲线C的极坐标方程为ρ=2sinθ-2cosθ．
（Ⅰ）求曲线C的普通方程；
（Ⅱ）当α=
π
4
时，求直线l被曲线C截得的弦长．
已知函数f（x）=sinx-2x+1，则f（tan
π
7
）+f（tan
6π
7
）=
 
．
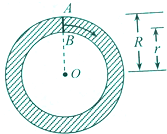如图，我们知道，圆环也可看作线段AB绕圆心O旋转一周所形成的平面图形，又圆环的面积S=π（R2-r2）=（R-r）×2π×
R+r
2
．所以，圆环的面积等于是以线段AB=R-r为宽，以AB中点绕圆心O旋转一周所形成的圆的周长2π×
R+r
2
为长的矩形面积．请将上述想法拓展到空间，并解决下列问题：若将平面区域M={（x，y）|（x-d）2+y2≤r2}（其中0＜r＜d）绕y轴旋转一周，则所形成的旋转体的体积是
 
．（结果用d，r表示）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网