题目内容
已知直线l的参数方程为:
(t为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ=2sinθ-2cosθ.
(Ⅰ)求曲线C的普通方程;
(Ⅱ)当α=
时,求直线l被曲线C截得的弦长.
|
(Ⅰ)求曲线C的普通方程;
(Ⅱ)当α=
| π |
| 4 |
考点:直线的参数方程,简单曲线的极坐标方程
专题:选作题,坐标系和参数方程
分析:(Ⅰ)根据极坐标和直角坐标的互化公式求得曲线C的直角坐标方程为 (x+1)2+(y-1)2=2;
(Ⅱ)当α=
时,直线l的方程为
,化成普通方程,并和曲线C的方程联立方程组,求得它们的交点坐标,即可求直线l被曲线C截得的弦长.
(Ⅱ)当α=
| π |
| 4 |
|
解答:
解:(Ⅰ)由ρ=2sinθ-2cosθ,可得ρ2=2ρsinθ-2ρcosθ
∴曲线C的直角坐标方程为x2+y2=2y-2x,
标准方程为:(x+1)2+(y-1)2=2;
(Ⅱ)当α=
时,直线l的方程为
,化成普通方程为y=x+2.
由
,解得
,或
.
∴直线l被曲线C截得的弦长为
=2
.
∴曲线C的直角坐标方程为x2+y2=2y-2x,
标准方程为:(x+1)2+(y-1)2=2;
(Ⅱ)当α=
| π |
| 4 |
|
由
|
|
|
∴直线l被曲线C截得的弦长为
| 4+4 |
| 2 |
点评:本题主要考查把参数方程、极坐标方程化为直角坐标方程的方法,求两个曲线的交点,属于基础题.

练习册系列答案
相关题目
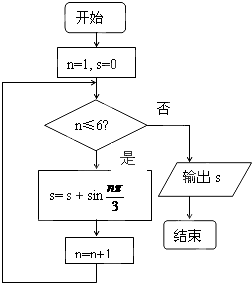
执行如图所示的程序框图,则输出的S的值为( )


| A、-7 | B、8 | C、-9 | D、-5 |
 如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为平行四边形,AD=A1A=
如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为平行四边形,AD=A1A=
 如图,在边长为a的正方形内有不规则图形Ω.向正方形内随机撒豆子,若撒在图形Ω内和正方形内的豆子数分别为m,n,则图形Ω面积的估计值为
如图,在边长为a的正方形内有不规则图形Ω.向正方形内随机撒豆子,若撒在图形Ω内和正方形内的豆子数分别为m,n,则图形Ω面积的估计值为