题目内容
已知函数f(x)=sinx-2x+1,则f(tan
)+f(tan
)= .
| π |
| 7 |
| 6π |
| 7 |
考点:函数奇偶性的性质,运用诱导公式化简求值
专题:函数的性质及应用
分析:根据正弦函数和正切函数是奇函数和tan
=-tan
,代入化简即可.
| 6π |
| 7 |
| π |
| 7 |
解答:
解:∵正弦函数是奇函数,
∴sin(-x)=-sinx
又tan
=-tan
,
∴f(tan
)+f(tan
)=f(tan
)+f(tan(-
))=sintan
-2tan
+1+sintan(-
)-2tan(-
)+1=2
故答案为:2
∴sin(-x)=-sinx
又tan
| 6π |
| 7 |
| π |
| 7 |
∴f(tan
| π |
| 7 |
| 6π |
| 7 |
| π |
| 7 |
| π |
| 7 |
| π |
| 7 |
| π |
| 7 |
| π |
| 7 |
| π |
| 7 |
故答案为:2
点评:本题考查了三角函数的奇偶性和三角函数的诱导公式,属于基础题.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
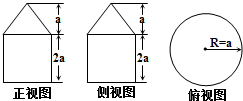 已知一个几何体的三视图如图所示,则此几何体的侧面积是( )
已知一个几何体的三视图如图所示,则此几何体的侧面积是( )| A、4πa2 | ||
| B、5πa2 | ||
C、(4+
| ||
D、(5+
|
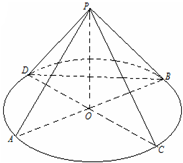 如图,AB,CD为圆O的两条直径,P为圆O所在平面外的一点,且PA=PB=PC
如图,AB,CD为圆O的两条直径,P为圆O所在平面外的一点,且PA=PB=PC
 如图,在边长为a的正方形内有不规则图形Ω.向正方形内随机撒豆子,若撒在图形Ω内和正方形内的豆子数分别为m,n,则图形Ω面积的估计值为
如图,在边长为a的正方形内有不规则图形Ω.向正方形内随机撒豆子,若撒在图形Ω内和正方形内的豆子数分别为m,n,则图形Ω面积的估计值为