题目内容
已知等差数列{an}的首项al=1,公差d>0,且第二项、第五项、第十四项分别是一个等比数列的第二项、第三项、第四项,
(1)求数列{an}的通项公式:
(2)设bn=
(n∈N*),Sn=b1+b2+…+bn是否存在最大的整数t,使得对任意的n均有Sn>
总成立?若存在,求出t:若不存在,请说明理由.
(1)求数列{an}的通项公式:
(2)设bn=
| 1 |
| n(an+5) |
| t |
| 36 |
考点:数列的求和,等差数列的通项公式
专题:等差数列与等比数列
分析:(1)由题意得(a1+d)(a1+13d)=(a1+4d)2,解得d,即可得出结论;
(2)利用裂项相消法求得sn,使得对任意的n均有Sn>
总成立,等价于sn的最小值大于
,即可得出结论.
(2)利用裂项相消法求得sn,使得对任意的n均有Sn>
| t |
| 36 |
| t |
| 36 |
解答:
解:(1)由题意得(a1+d)(a1+13d)=(a1+4d)2,
整理得2a1d=d2,
∵a1=1,解得:d=0(舍),d=2,
∴an=2n-1(n∈N*).
(2)bn=
=
=
(
-
),
∴Sn=b1+b2+…+bn=
(1-
+
-
+
-
+…+
-
)
=
(1+
-
-
)=
-
,
∴sn+1-sn=
(
-
)>0,
∴数列{Sn}是单调递增的,∴s1=
∴使得对任意的n均有Sn>
总成立,等价于
>
,即t<6,
又∵t∈N*,∴满足条件的t的最大值是5.
整理得2a1d=d2,
∵a1=1,解得:d=0(舍),d=2,
∴an=2n-1(n∈N*).
(2)bn=
| 1 |
| n(an+5) |
| 1 |
| 2n(n+2) |
| 1 |
| 4 |
| 1 |
| n |
| 1 |
| n+2 |
∴Sn=b1+b2+…+bn=
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| n |
| 1 |
| n+2 |
=
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| n+1 |
| 1 |
| n+2 |
| 3 |
| 8 |
| 2n+3 |
| 4(n+1)(n+2) |
∴sn+1-sn=
| 1 |
| 4 |
| 1 |
| n+1 |
| 1 |
| n+3 |
∴数列{Sn}是单调递增的,∴s1=
| 1 |
| 6 |
∴使得对任意的n均有Sn>
| t |
| 36 |
| 1 |
| 6 |
| t |
| 36 |
又∵t∈N*,∴满足条件的t的最大值是5.
点评:本题主要考查等差数列、等比数列的性质及裂项法求数列的和知识,考查学生恒成立问题的等价转化能力及运算求解能力,属难题.

练习册系列答案
相关题目
某几何体的三视图如图所示,则该几何体的表面积为( )


| A、20π | B、16π |
| C、12π | D、10π |
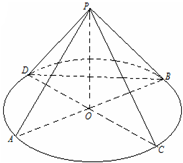 如图,AB,CD为圆O的两条直径,P为圆O所在平面外的一点,且PA=PB=PC
如图,AB,CD为圆O的两条直径,P为圆O所在平面外的一点,且PA=PB=PC 如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为平行四边形,AD=A1A=
如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为平行四边形,AD=A1A=