题目内容
已知实数x、y、z满足2x2+3y2+6z2=a(a>0),且x+y+z的最大值是1,求a的值.
考点:柯西不等式的几何意义
专题:综合题,不等式
分析:由柯西不等式:[(
x)2+(
y)2+(
z)2][(
)2+(
)2+(
)2]≥(
×
x+
×
y+
×
z)2,可得出x+y+z的最大值,从而可根据最大值为1,建立关于a的方程解出a值即可.
| 2 |
| 3 |
| 6 |
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| 2 |
| 1 | ||
|
| 3 |
| 1 | ||
|
| 6 |
解答:
解:由柯西不等式:[(
x)2+(
y)2+(
z)2][(
)2+(
)2+(
)2]≥(
×
x+
×
y+
×
z)2…(5分)
因为2x2+3y2+6z2=a(a>0),所以a≥(x+y+z)2,
因为x+y+z的最大值是1,所以a=1,
当2x=3y=6z时,x+y+z取最大值,…(6分)
所以a=1.…(7分)
| 2 |
| 3 |
| 6 |
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| 2 |
| 1 | ||
|
| 3 |
| 1 | ||
|
| 6 |
因为2x2+3y2+6z2=a(a>0),所以a≥(x+y+z)2,
因为x+y+z的最大值是1,所以a=1,
当2x=3y=6z时,x+y+z取最大值,…(6分)
所以a=1.…(7分)
点评:本小题主要考查柯西不等式等基础知识,考查运算求解能力,对于柯西不等式的构造是题目的关键,需要同学们灵活应用.

练习册系列答案
相关题目
已知f(x)=sinωx+
cosωx(ω>0)的两条相邻的对称轴间的距离为
,且f(x)图象关于点(x0,0)成中心对称,则x0可能为( )
| 3 |
| π |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
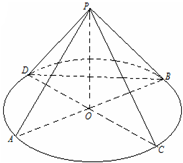 如图,AB,CD为圆O的两条直径,P为圆O所在平面外的一点,且PA=PB=PC
如图,AB,CD为圆O的两条直径,P为圆O所在平面外的一点,且PA=PB=PC 如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为平行四边形,AD=A1A=
如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为平行四边形,AD=A1A= 如图,在边长为a的正方形内有不规则图形Ω.向正方形内随机撒豆子,若撒在图形Ω内和正方形内的豆子数分别为m,n,则图形Ω面积的估计值为
如图,在边长为a的正方形内有不规则图形Ω.向正方形内随机撒豆子,若撒在图形Ω内和正方形内的豆子数分别为m,n,则图形Ω面积的估计值为