题目内容
抛掷一枚质地不均匀的骰子,出现向上点数为1,2,3,4,5,6的概率依次记为p1,p2,p3,p4,p5,p6,经统计发现,数列{pn}恰好构成等差数列,且p4是p1的3倍.
(Ⅰ)求数列{pn}的通项公式.
(Ⅱ)甲、乙两人用这枚骰子玩游戏,并规定:掷一次骰子后,若向上点数为奇数,则甲获胜,否则已获胜,请问这样的规则对甲、乙二人是否公平?请说明理由;
(Ⅲ)甲、乙、丙三人用这枚骰子玩游戏,根据掷一次后向上的点数决定胜出者,并制定了公平的游戏方案,试在下面的表格中列举出两种可能的方案(不必证明).
(Ⅰ)求数列{pn}的通项公式.
(Ⅱ)甲、乙两人用这枚骰子玩游戏,并规定:掷一次骰子后,若向上点数为奇数,则甲获胜,否则已获胜,请问这样的规则对甲、乙二人是否公平?请说明理由;
(Ⅲ)甲、乙、丙三人用这枚骰子玩游戏,根据掷一次后向上的点数决定胜出者,并制定了公平的游戏方案,试在下面的表格中列举出两种可能的方案(不必证明).
| 方案序号 | 甲胜出对应点数 | 乙胜出对应点数 | 丙胜出对应点数 |
| ① | |||
| ② |
考点:互斥事件的概率加法公式,古典概型及其概率计算公式
专题:概率与统计
分析:(Ⅰ)设数列{pn}的公差为d,由p4是p1的3倍及概率的性质,得到方程,解方程,继而求得通项公式.
(Ⅱ)分别求出甲乙的概率,然后比较即可.
(Ⅲ)根据投掷的点数写出所有的可能即可.
(Ⅱ)分别求出甲乙的概率,然后比较即可.
(Ⅲ)根据投掷的点数写出所有的可能即可.
解答:
解:(Ⅰ)设数列{pn}的公差为d,由p4是p1的3倍及概率的性质,有
,
解得P1=
,d=
,
故Pn=
,1≤n≤6,n∈N*
(Ⅱ)不公平,
甲获胜的概率P甲=p1+p2+p3=
=
,
甲获胜的概率PP乙=p4+p5+p6=
=
,
二者概率不同,所以不公平.
(Ⅲ)(共6种可能,答出任意2种即可)
|
解得P1=
| 1 |
| 16 |
| 1 |
| 24 |
故Pn=
| 2n+1 |
| 48 |
(Ⅱ)不公平,
甲获胜的概率P甲=p1+p2+p3=
| 3+7+11 |
| 48 |
| 7 |
| 16 |
甲获胜的概率PP乙=p4+p5+p6=
| 5+9+13 |
| 48 |
| 9 |
| 16 |
二者概率不同,所以不公平.
(Ⅲ)(共6种可能,答出任意2种即可)
| 甲获胜对应点数 | 乙获胜对应点数 | 丙获胜对应点数 | |
| ① | 1,6 | 2,5 | 3,4 |
| ② | 1,6 | 3,4 | 2,5 |
| ③ | 2,5 | 3,4 | 1,6 |
| ④ | 2,5 | 1,6 | 3,4 |
| ⑤ | 3,4 | 1,6 | 2,5 |
| ⑥ | 3,4 | 2,5 | 1,6 |
点评:本题主要考查了等差数列的通项公式,概率的求法,属于基础题.

练习册系列答案
相关题目
已知tan2α=
,α∈(0,
),则
=( )
| 3 |
| 4 |
| π |
| 4 |
| sinα+cosα |
| sinα-cosα |
| A、1 | B、-1 | C、2 | D、-2 |
已知f(x)=sinωx+
cosωx(ω>0)的两条相邻的对称轴间的距离为
,且f(x)图象关于点(x0,0)成中心对称,则x0可能为( )
| 3 |
| π |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
某几何体的三视图如图所示,则该几何体的表面积为( )


| A、20π | B、16π |
| C、12π | D、10π |
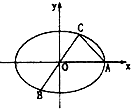 如图,已知椭圆
如图,已知椭圆 已知椭圆C:
已知椭圆C: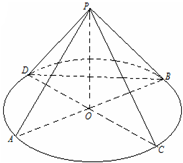 如图,AB,CD为圆O的两条直径,P为圆O所在平面外的一点,且PA=PB=PC
如图,AB,CD为圆O的两条直径,P为圆O所在平面外的一点,且PA=PB=PC