题目内容
已知集合A={x|
≤0}，B={x|x2-7x+10＜0}，则∁R（A∩B）=（ ）
| x-3 |
| x-7 |
| A、（-∞，3）∪（5，+∞） |
| B、（-∞，3）∪[5，+∞） |
| C、（-∞，3]∪[5，+∞） |
| D、（-∞，3]∪（5，+∞） |
考点：交、并、补集的混合运算
专题：集合
分析：解分式不等式求得A，解一元二次不等式求得B，根据两个集合的交集的定义求得 A∩B，再根据补集的定义求得∁R（A∩B）．
解答：
解：集合A={x|
≤0}={x|3≤x＜7}，B={x|x2-7x+10＜0}={x|2＜x＜5}，
∴A∩B=[3，5），
∴∁R（A∩B）=（-∞，3）∪[5，+∞），
故选：B．
| x-3 |
| x-7 |
∴A∩B=[3，5），
∴∁R（A∩B）=（-∞，3）∪[5，+∞），
故选：B．
点评：本题主要考查分式不等式、一元二次不等式的解法，补集、两个集合的交集的定义和求法，属于基础题．
练习册系列答案
相关题目
数列{an}为等比数列，若a4=1，a12=16，则a8的值为（ ）
| A、±4 | ||
| B、-4 | ||
| C、4 | ||
D、4
|
4名优秀学生A、B、C、D全部都被保送到甲、乙、丙3所学校，每所学校至少去一名，则不同的保送方案共有（ ）
| A、18种 | B、36种 |
| C、72种 | D、108种 |
执行如图所示的程序框图，若输出的结果为2，则输入的正整数a的可能取值的集合是（ ）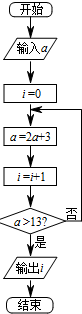
| A、{1，2，3，4，5} |
| B、{1，2，3，4，5，6} |
| C、{2，3，4，5} |
| D、{2，3，4，5，6} |
已知
=（2，1），
=（-1，k），如果
∥
，则实数k的值等于（ ）
| a |
| b |
| a |
| b |
| A、2 | ||
| B、-2 | ||
C、
| ||
D、-
|
已知复数z1=2+i，z2=a-3i（i为虚数单位，a∈R）．若z1•z2为实数，则a的值为（ ）
| A、3 | B、4 | C、5 | D、6 |
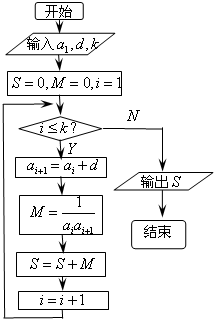已知数列{an}的各项均为正数，观察程序框图，当k=2时，S=