Question

设函数f（x）=sin（ωx-

3π

4

）（ω＞0）的最小正周期为π
（Ⅰ）求ω；
（Ⅱ）若f（

α

2

+

3π

8

）=

24

25

，且α∈（-

π

2

，

π

2

），求tanα的值．
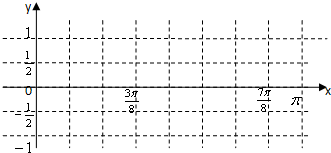
（Ⅲ）画出函数y=f（x）在区间[0，π]上的图象（完成列表并作图）．
（1）列表

x	0		3π 8		7π 8	π
y		-1		1

（2）描点，连线

Answer 1

考点：五点法作函数y=Asin（ωx+φ）的图象,函数y=Asin（ωx+φ）的图象变换,由y=Asin（ωx+φ）的部分图象确定其解析式

专题：三角函数的图像与性质

分析：（Ⅰ）利用函数的周期公式直接求ω；
（Ⅱ）通过f（

α

2

+

3π

8

）=

24

25

，且α∈（-

π

2

，

π

2

），求出sinα，利用三角函数的基本关系式即可求tanα的值．
（Ⅲ）结合表格，通过函数的解析式，直接填补，画出函数y=f（x）在区间[0，π]上的图象（完成列表并作图）．

解答： 解：（Ⅰ）∵函数f(x)=sin(ωx-

3π

4

)(ω＞0)的最小正周期为π，
∴

2π

ω

=π，
∴ω=2．…（2分）
（Ⅱ）由（Ⅰ）知f(x)=sin(2x-

3π

4

)
由f(

α

2

+

3π

8

)=

24

25

得：sinα=

24

25

，…（4分）
∵-

π

2

＜α＜

π

2

∴cosα=

7

25

…（6分）
∴tanα=

24

7

．  …（8分）
（其他写法参照给分）
（Ⅲ）由（Ⅰ）知f(x)=sin(2x-

3π

4

)，于是有
（1）列表

x	0	π 8	3π 8	x∈[0， π 2 ]	7π 8	a，b
y	- 2 2	-1	0	1	0	- 2 2

…（11分）
（2）描点，连线函数y=f（x）在区间[0，π]上图象如下…（14分）

点评：本题考查三角函数的解析式的求法，函数的图象的画法，基本性质以及基本知识的考查．