题目内容
已知椭圆Σ的两个焦点分别是F1(-2,0)、F2(2,0),并且经过点P(
,-
).
(1)求椭圆Σ的标准方程;
(2)求∠F1PF2的平分线所在直线的方程.
| 5 |
| 2 |
| 3 |
| 2 |
(1)求椭圆Σ的标准方程;
(2)求∠F1PF2的平分线所在直线的方程.
考点:椭圆的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:(1)利用椭圆的定义,即可求椭圆Σ的标准方程;
(2)(方法一)利用向量法,(方法二)利用角平分线的性质,可求∠F1PF2的平分线所在直线的方程.
(2)(方法一)利用向量法,(方法二)利用角平分线的性质,可求∠F1PF2的平分线所在直线的方程.
解答:
解:(1)依题意,设椭圆Σ的标准方程为
+
=1(a>b>0)…(1分)c=2…(2分),2a=
+
=2
…(4分)
所以a=
,b=
=
…(5分)
椭圆Σ的标准方程为
+
=1…(6分)
(2)由图可知,∠F1PF2的平分线与x轴相交,设交点为Q(m,0)…(7分)
(方法一)
=(m-
,
),
=(-
,
),
=(-
,
)…(8分)
依题意,∠F1PQ=∠F2PQ,cos∠F1PQ=cos∠F2PQ,
=
…(10分)
即
=
…(11分)
解得m=1…(12分)
角平分线PQ所在直线的方程为
=
,即x+y-1=0…(13分)
(方法二)|PF1|=
=
,|PF2|=
…(8分)
因为PQ是角平分线,所以
=
…(10分)
即
=
…(11分)
解得m=1…(12分)
角平分线PQ所在直线的方程为
=
,即x+y-1=0…(13分)
| x2 |
| a2 |
| y2 |
| b2 |
(-2-
|
(2-
|
| 10 |
所以a=
| 10 |
| a2-c2 |
| 6 |
椭圆Σ的标准方程为
| x2 |
| 10 |
| y2 |
| 6 |
(2)由图可知,∠F1PF2的平分线与x轴相交,设交点为Q(m,0)…(7分)
(方法一)
| PQ |
| 5 |
| 2 |
| 3 |
| 2 |
| PF1 |
| 9 |
| 2 |
| 3 |
| 2 |
| PF2 |
| 1 |
| 2 |
| 3 |
| 2 |
依题意,∠F1PQ=∠F2PQ,cos∠F1PQ=cos∠F2PQ,
| ||||
|
|
| ||||
|
|
即
-
| ||||||||||
|
-
| ||||||||||
|
解得m=1…(12分)
角平分线PQ所在直线的方程为
| y-0 | ||
-
|
| x-1 | ||
|
(方法二)|PF1|=
(
|
| 3 |
| 2 |
| 10 |
| 1 |
| 2 |
| 10 |
因为PQ是角平分线,所以
| |PF1| |
| |PF2| |
| |QF1| |
| |QF2| |
即
| 3 |
| 1 |
| m+2 |
| m-2 |
解得m=1…(12分)
角平分线PQ所在直线的方程为
| y-0 | ||
-
|
| x-1 | ||
|
点评:本题考查椭圆的方程与性质,考查椭圆的定义,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
已知x=
与x=
为函数f(x)=3sin(ωx+
)的两条相邻对称轴,则ω=( )
| π |
| 4 |
| 3π |
| 4 |
| π |
| 6 |
| A、1 | B、2 | C、±1 | D、±2 |
不等式|2x-1|≤3的解集为( )
| A、{x|-1≤x≤2} |
| B、{x|x≥2或x≤-1} |
| C、{x|-2≤x≤1} |
| D、{x|x≥1或x≤-2} |
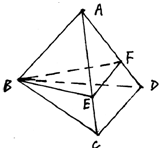 已知正三棱锥A-BCD中,底面边长为a,侧棱长为2a,过B点作与则棱AC、AD相交的截面BEF,在这个截面三角形中,求:
已知正三棱锥A-BCD中,底面边长为a,侧棱长为2a,过B点作与则棱AC、AD相交的截面BEF,在这个截面三角形中,求: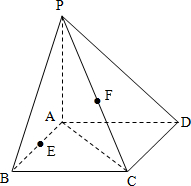 已知PA⊥平面ABCD,四边形ABCD为正方形,PA=AB=4,E、F分别为AB、PC的中点.
已知PA⊥平面ABCD,四边形ABCD为正方形,PA=AB=4,E、F分别为AB、PC的中点.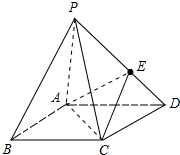 如图,底面是平行四边形的四棱锥P-ABCD,点E在PD上,且PE:ED=2:1,问:在棱PC上是否存在一点F,使BF∥平面AEC?证明你的结论.
如图,底面是平行四边形的四棱锥P-ABCD,点E在PD上,且PE:ED=2:1,问:在棱PC上是否存在一点F,使BF∥平面AEC?证明你的结论.