题目内容
已知x=
与x=
为函数f（x）=3sin（ωx+
）的两条相邻对称轴，则ω=（ ）
| π |
| 4 |
| 3π |
| 4 |
| π |
| 6 |
| A、1 | B、2 | C、±1 | D、±2 |
考点：函数y=Asin（ωx+φ）的图象变换
专题：三角函数的图像与性质
分析：由三角函数的性质可得函数的半周期为
-
，由周期公式可解ω
| 3π |
| 4 |
| π |
| 4 |
解答：
解：∵x=
与x=
为函数f（x）=3sin（ωx+
）的两条相邻对称轴，
∴函数的半周期为
-
=
，∴
=π，
解得ω=±2
故选：D
| π |
| 4 |
| 3π |
| 4 |
| π |
| 6 |
∴函数的半周期为
| 3π |
| 4 |
| π |
| 4 |
| π |
| 2 |
| 2π |
| |ω| |
解得ω=±2
故选：D
点评：本题考查三角函数的图象和性质，得出函数的周期是解决问题的关键，属基础题．
练习册系列答案
阅读快车系列答案
相关题目
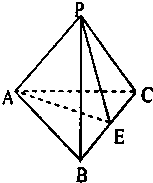如图所示，点P是平面ABC外一点，且满足PA、PB、PC两两垂直，PE⊥BC，则该图中两两垂直的平面共有（ ）| A、3对 | B、4对 | C、5对 | D、6对 |
极坐标平面内，集合P={（ρ，θ）|sinθ=-
，ρ∈R}与集合S={（ρ，θ）|cosθ=
，ρ∈R}之间的关系是（ ）
| 1 |
| 2 |
| ||
| 2 |
| A、P?S |
| B、P?S |
| C、P=S |
| D、P∩S={（0，0）} |
下列推理是归纳推理的是（ ）
| A、A，B为定点，动点P满足|PA|+|PB|=2a＞|AB|，得P的轨迹为椭圆 | ||||
| B、科学家利用鱼的沉浮原理制造潜艇 | ||||
C、由圆x2+y2=r2的面积πr2，猜出椭圆
| ||||
| D、由a1=1，an=3n-1，求出S1，S2，S3，猜想出数列的前n项和Sn的表达式 |
下列命题正确的个数是（ ）
（1）有两个面互相平行，其余各面都是平行四边形的几何体是棱柱
（2）棱柱的底面一定是平行四边形
（3）棱锥被平面分成的两部分不可能都是棱锥
（4）用平行于圆锥底面的平面去截这个圆锥，所得几何体叫做圆台．
（1）有两个面互相平行，其余各面都是平行四边形的几何体是棱柱
（2）棱柱的底面一定是平行四边形
（3）棱锥被平面分成的两部分不可能都是棱锥
（4）用平行于圆锥底面的平面去截这个圆锥，所得几何体叫做圆台．
| A、0 | B、1 | C、2 | D、3 |
已知函数f（x）=
，满足?x1≠x2，都有
＜0成立，则a的取值范围是（ ）
|
| f(x1)-f(x2) |
| x1-x2 |
| A、（0，1） | ||
| B、（1，+∞） | ||
C、（0，
| ||
D、（0，
|
| ∫ | 1 0 |
| 1-(x-1)2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、1-
|
两条异面直线指的是（ ）
| A、没有公共点的两条直线 |
| B、分别位于两个不同平面的两条直线 |
| C、某一平面内的一条直线和这个平面外的一条直线 |
| D、不同在任何一个平面内的两条直线 |