题目内容
已知函数y=x2+alnx+
在(1,4)上单调递减,求a的取值范围.
| 2 |
| x |
考点:利用导数研究函数的单调性
专题:导数的综合应用
分析:求函数的导数,利用函数单调性和导数之间的关系即可得到结论.
解答:
解:函数的导数为y′=2x+
-
,
若函数y=x2+alnx+
在(1,4)上单调递减,
则函数y′=2x+
-
≤0在(1,4)恒成立,
即a≤
-2x2在(1,4)恒成立,
∵函数f(x)=
-2x2的导数f′(x)=-
-4x<0,
∴函数在(1,4)上单调递减,
∴f(4)<f(x)<f(1),
即-
<f(x)<0,
则a≤-
.
| a |
| x |
| 2 |
| x2 |
若函数y=x2+alnx+
| 2 |
| x |
则函数y′=2x+
| a |
| x |
| 2 |
| x2 |
即a≤
| 2 |
| x |
∵函数f(x)=
| 2 |
| x |
| 2 |
| x2 |
∴函数在(1,4)上单调递减,
∴f(4)<f(x)<f(1),
即-
| 15 |
| 2 |
则a≤-
| 15 |
| 2 |
点评:本题主要考查函数单调性和导数之间的关系,将函数的单调性转化为函数最值恒成立是解决本题的关键.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
下列命题正确的个数是( )
(1)有两个面互相平行,其余各面都是平行四边形的几何体是棱柱
(2)棱柱的底面一定是平行四边形
(3)棱锥被平面分成的两部分不可能都是棱锥
(4)用平行于圆锥底面的平面去截这个圆锥,所得几何体叫做圆台.
(1)有两个面互相平行,其余各面都是平行四边形的几何体是棱柱
(2)棱柱的底面一定是平行四边形
(3)棱锥被平面分成的两部分不可能都是棱锥
(4)用平行于圆锥底面的平面去截这个圆锥,所得几何体叫做圆台.
| A、0 | B、1 | C、2 | D、3 |
已知不等式x2-x≤0的解集为M,且集合N={x|
<0},则M∩N为( )
| x+1 |
| x-1 |
| A、[0,1) |
| B、(0,1) |
| C、[0,1] |
| D、(-1,0] |
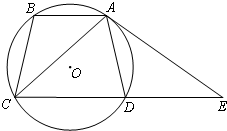 如图,等腰梯形ABCD内接于⊙O,AB∥CD.过点A作⊙O的切线交CD的延长线于点E.求证:∠DAE=∠BAC.
如图,等腰梯形ABCD内接于⊙O,AB∥CD.过点A作⊙O的切线交CD的延长线于点E.求证:∠DAE=∠BAC. 如图,长方体ABCD-A1B1C1D1中,AB=BC=a,AA1=2a.
如图,长方体ABCD-A1B1C1D1中,AB=BC=a,AA1=2a.