题目内容

已知定点F（1，0），动点P（异于原点）在y轴上运动，连结PF，过点P作PM交x轴于点M，并延长MP与N，且
PM
•
PF
=0，|
PN
|=|
PM
|．
（1）求动点N的轨迹C的方程；
（2）若A（a，0），a∈R，求使|
AN
|最小的点N的坐标．
考点：轨迹方程
专题：综合题,圆锥曲线的定义、性质与方程
分析：（1）设出动点N，则M，P的坐标可表示出，利用PM⊥PF，kPMkPF=-1，求得x和y的关系式，即N的轨迹方程；
（2）设x=t2，则|
AN
|=
(x-a)2+y2
，利用配方法即可求解．
解答： 解：（1）设动点N（x，y），则M（-x，0），P（0，
y
2
）（x＞0），
∵
PM
•
PF
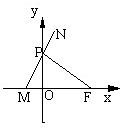
=0，∴PM⊥PF，∴kPMkPF=-1，即
y
2
x
•
y
2
-1
=-1，
∴y2=4x（x＞0）即为所求；
（2）设x=t2，则|
AN
|=
(x-a)2+y2
=
(t2-a)2+4t2
=
5(t2-
a
5
)2+
4
5
a2
，
∴t2=
a
5
时，|
AN
|最小．
此时得：N（
a
5
，±
2
a
5
）．
点评：本题主要考查了直线与圆锥曲线的综合问题，两个向量的数量的运算，考查运用解析几何的方法分析问题和解决问题的能力，属于中档题．
练习册系列答案
相关题目
执行如图所示的程序框图，如输入的p=20，则输出的n的值是（　　）
A、3B、4C、5D、6
已知某物体的运动曲线方程为：S=2t2-3t-1，则该物体在t=3时的速度为（　　）
A、8B、9C、10D、11
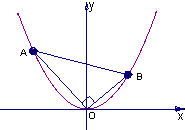在平面直角坐标系xOy中，抛物线y=x2上异于坐标原点O的两不同动点A、B满足AO⊥BO
（Ⅰ）求证直线A、B恒过定点（0，1）
（Ⅱ）△AOB的面积是否存在最小值？若存在，请求出最小值；若不存在，请说明理由．
若两圆x2+y2=9与x2+y2-8x+6y-8a-25=0存在唯一公共点，求实数a的值．
在△ABC中，角A，B，C所对应的边分别为a，b，c，tan
A+B
2
+tan
C
2
=4，2sinBcosC=sinA．
（1）求角A的大小；
（2）若S△ABC=
3
，求边a的大小．
设向量
a
=（a1，a2），
b
=（b1，b2），定义一种向量积
a
?
b
=（a1，a2）?（b1，b2）=（a1b1，a2b2）．已知向量
m
=（2，
1
2
），
n
=（
π
3
，0），点P（x0，y0）为y=sinx的图象上的动点，点Q（x，y）为y=f（x）的图象上的动点，且满足
OQ
=
m
?
OP
+
n
（其中O为坐标原点）．
（Ⅰ）请用x0表示
m
?
OP
；
（Ⅱ）求y=f（x）的表达式并求它的周期；
（Ⅲ）把函数y=f（x）图象上各点的横坐标缩小为原来的
1
4
倍（纵坐标不变），得到函数y=g（x）的图象．设函数h（x）=g（x）-t（t∈R），试讨论函数h（x）在区间[0，
π
2
]内的零点个数．
已知A={-1，1}，B={x|x2+mx+n=0}，B≠∅且B⊆A，求实数m，n的值．
若△ABC中a=
7
b，sinC=2
3
sinB，则A=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网