题目内容
已知在△ABC中,角A,B,C 的对边分别是a,b,c,若a=6,b=5,cosC=
(1)求边长c的大小;
(2)求三角形ABC的面积.
| 4 |
| 5 |
(1)求边长c的大小;
(2)求三角形ABC的面积.
考点:余弦定理,正弦定理
专题:解三角形
分析:(1)利用余弦定理,把已知条件代入c2=a2+b2-2abcosC求值;
(2)根据cosC=
和平方关系求出sinC的值,再代入三角形的面积公式求值.
(2)根据cosC=
| 4 |
| 5 |
解答:
解:(1)由余弦定理得,
c2=a2+b2-2abcosC=36+25-2×6×5×
=13,
解得c=
-----------------------------------(6分)
(2)因为cosC=
,且C是内角,所以sinC=
=
,
所以S△ABC=
•absinC=
×6×5×
=9------------------(12分)
c2=a2+b2-2abcosC=36+25-2×6×5×
| 4 |
| 5 |
解得c=
| 13 |
(2)因为cosC=
| 4 |
| 5 |
| 1-cos2C |
| 3 |
| 5 |
所以S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 5 |
点评:本题考查余弦定理,平方关系,以及三角形的面积公式的应用,熟练掌握公式是解题的关键.

练习册系列答案
相关题目
在R上定义运算?:x?y=x(l-y).若对任意x>2,不等式(x-a)?x≤a+2都成立,则实数a的取值范围是( )
| A、[一1,7] |
| B、(一∞,3] |
| C、(一∞,7] |
| D、(一∞,-1]U[7,+∞) |
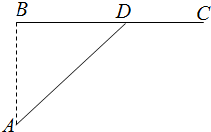 如图,已知海岛A到海岸公路BC的距离AB=50km,B,C间的距离为100km,从A到C必须先坐船到BC上的某一点D,航速为25km/h,再乘汽车到C,车速为50km/h,记∠BDA=θ
如图,已知海岛A到海岸公路BC的距离AB=50km,B,C间的距离为100km,从A到C必须先坐船到BC上的某一点D,航速为25km/h,再乘汽车到C,车速为50km/h,记∠BDA=θ