题目内容
5.某租车公司给出的财务报表如下: | 1014年(1-12月) | 1015年(1-12月) | 1016年(1-11月) |
| 接单量(单) | 14463272 | 40125125 | 50331996 |
| 油费(元) | 214301962 | 591305364 | 653214963 |
| 平均每单油费t(元) | 14.82 | 14.49 | |
| 平均每单里程k(公里) | 15 | 15 | |
| 每公里油耗a(元) | 0.7 | 0.7 | 0.7 |
(1)分别计算2014,2015年该公司的空驶率的值(精确到0.01%);
(2)2016年该公司加强了流程管理,利用租车软件,降低了空驶率并提高了平均每单里程,核算截止到11月30日,空驶率在2015年的基础上降低了20个百分点,问2016年前11个月的平均每单油费和平均每单里程分别为多少?(分别精确到0.01元和0.01公里)
分析 (1)根据空驶率的计算公式为$T=\frac{t-ak}{ak}•100%$,带入计算即可;(2)根据T2016的值,求出k的值,从而求出2016年前11个月的平均每单油费和平均每单里程.
解答 解:(1)${T_{2014}}=\frac{14.82-0.7×15}{0.7×15}•100%≈41.14%$,
${T_{2015}}=\frac{14.49-0.7×15}{0.7×15}•100%≈38.00%$,
∴2014、2015年,该公司空驶率分别为41.14%和38.00%.
(2)${t_{2016}}=\frac{653214963}{50331996}≈12.98$,T2016=38%-20%=18%.
由${T_{2016}}=\frac{12.98-0.7k}{0.7k}•100%≈18.00%⇒k=15.71$,
∴2016年前11个月的平均每单油费为12.98元,
平均每单里程为15.71km.
点评 本题考查了函数模型问题,考查代入求值,是一道中档题.

练习册系列答案
相关题目
15.若x∈R,则(1-|x|)(1+x)>0的解集是( )
| A. | {x|0≤x<1} | B. | {x|x<0且x≠-1} | C. | {x|-1<x<1} | D. | {x|x<1且x≠-1} |
20.设x,y∈R,则“|x|+|y|>1”的一个充分条件是( )
| A. | |x|≥1 | B. | |x+y|≥1 | C. | y≤-2 | D. | $|x|≥\frac{1}{2}$且$|y|≥\frac{1}{2}$ |
10.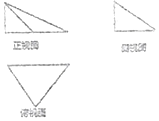 一个几何体的三视图如图所示,其中俯视图是一个腰长为2的等腰直角三角形,侧视图是一个直角边长为1的直角三角形,则该几何体外接球的体积是( )
一个几何体的三视图如图所示,其中俯视图是一个腰长为2的等腰直角三角形,侧视图是一个直角边长为1的直角三角形,则该几何体外接球的体积是( )
 一个几何体的三视图如图所示,其中俯视图是一个腰长为2的等腰直角三角形,侧视图是一个直角边长为1的直角三角形,则该几何体外接球的体积是( )
一个几何体的三视图如图所示,其中俯视图是一个腰长为2的等腰直角三角形,侧视图是一个直角边长为1的直角三角形,则该几何体外接球的体积是( )| A. | 36π | B. | 9π | C. | $\frac{9}{2}π$ | D. | $\frac{27}{5}π$ |
14.复数$z=\frac{i}{1-i}$的共轭复数的模为( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | 1 | D. | 2 |