题目内容
20.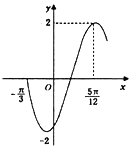 函数$f(x)=2sin({ωx+φ})({ω>0,-\frac{π}{2}<ω<\frac{π}{2}})$的部分图象如图所示,将f(x)的图象向左平移$\frac{π}{6}$个单位后的解析式为y=2sin2x.
函数$f(x)=2sin({ωx+φ})({ω>0,-\frac{π}{2}<ω<\frac{π}{2}})$的部分图象如图所示,将f(x)的图象向左平移$\frac{π}{6}$个单位后的解析式为y=2sin2x.
分析 由函数的图象求出T,由周期求出ω,由五点法作图求出φ的值,可得函数的解析式.再根据函数y=Asin(ωx+φ)的图象变换规律,可得结论.
解答 解:由函数的图象可得$\frac{3}{4}$T=$\frac{5π}{12}$-(-$\frac{π}{3}$)=$\frac{3π}{4}$,可得:T=π=$\frac{2π}{ω}$,
∴ω=2.
再根据点($\frac{5π}{12}$,2)在函数图象上,可得:2sin(2×$\frac{5π}{12}$+φ)=2,
∴2×$\frac{5π}{12}$+φ=2kπ+$\frac{π}{2}$,k∈Z,解得:φ=2kπ-$\frac{π}{3}$,k∈Z,
∴函数f(x)=2sin(2x-$\frac{π}{3}$).
把函数f(x)=2sin(2x-$\frac{π}{3}$)的图象向左平移$\frac{π}{6}$个单位,可得y=2sin[2(x+$\frac{π}{6}$)-$\frac{π}{3}$]=2sin2x的图象,
故答案为:y=2sin2x.
点评 本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,函数y=Asin(ωx+φ)的图象变换规律,属于基础题.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
10.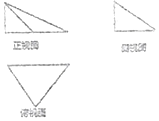 一个几何体的三视图如图所示,其中俯视图是一个腰长为2的等腰直角三角形,侧视图是一个直角边长为1的直角三角形,则该几何体外接球的体积是( )
一个几何体的三视图如图所示,其中俯视图是一个腰长为2的等腰直角三角形,侧视图是一个直角边长为1的直角三角形,则该几何体外接球的体积是( )
 一个几何体的三视图如图所示,其中俯视图是一个腰长为2的等腰直角三角形,侧视图是一个直角边长为1的直角三角形,则该几何体外接球的体积是( )
一个几何体的三视图如图所示,其中俯视图是一个腰长为2的等腰直角三角形,侧视图是一个直角边长为1的直角三角形,则该几何体外接球的体积是( )| A. | 36π | B. | 9π | C. | $\frac{9}{2}π$ | D. | $\frac{27}{5}π$ |
11.若集合A={0,1,2,4},B={1,2,3},则A∩B=( )
| A. | {0,1,2,3,4} | B. | {0,1} | C. | {0,1,4} | D. | {1,2} |
8.椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{2}$=1(a>0)的长轴长为4,则C的离心率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\sqrt{2}$ |
5.将函数$y=3sin(2x+\frac{π}{6})$的图象上各点沿x轴向右平移$\frac{π}{6}$个单位长度,所得函数图象的一个对称中心为( )
| A. | $(\frac{7π}{12},0)$ | B. | $(\frac{π}{6},0)$ | C. | $(\frac{5π}{8},0)$ | D. | $(\frac{2π}{3},-3)$ |
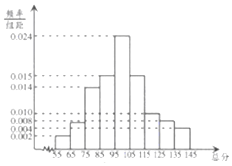 从某市统考的学生数学考试卷中随机抽查100份数学试卷作为样本,分别统计出这些试卷总分,由总分得到如下的频率分布直方图.
从某市统考的学生数学考试卷中随机抽查100份数学试卷作为样本,分别统计出这些试卷总分,由总分得到如下的频率分布直方图.