题目内容
19.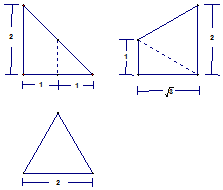 如图是某空间几何体的三视图其中主视图、侧视图、俯视图依次为直角三角形、直角梯形、等边三角形,则该几何体的体积( )
如图是某空间几何体的三视图其中主视图、侧视图、俯视图依次为直角三角形、直角梯形、等边三角形,则该几何体的体积( )| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{2\sqrt{3}}}{3}$ | D. | $\sqrt{3}$ |
分析 如图所示,该几何体为四棱锥,其中侧面ACBD⊥底面PAB.侧面ACBD为直角梯形,PA⊥AB.
解答 解:如图所示, 该几何体为四棱锥,其中侧面ACBD⊥底面PAB.
该几何体为四棱锥,其中侧面ACBD⊥底面PAB.
侧面ACBD为直角梯形,
PA⊥AB.
该几何体的体积V=$\frac{1}{3}×\frac{1+2}{2}×2×\sqrt{3}$=$\sqrt{3}$.
故选:D.
点评 本题考查了四棱锥的三视图、等边三角形与直角梯形的面积计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
10.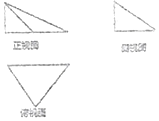 一个几何体的三视图如图所示,其中俯视图是一个腰长为2的等腰直角三角形,侧视图是一个直角边长为1的直角三角形,则该几何体外接球的体积是( )
一个几何体的三视图如图所示,其中俯视图是一个腰长为2的等腰直角三角形,侧视图是一个直角边长为1的直角三角形,则该几何体外接球的体积是( )
 一个几何体的三视图如图所示,其中俯视图是一个腰长为2的等腰直角三角形,侧视图是一个直角边长为1的直角三角形,则该几何体外接球的体积是( )
一个几何体的三视图如图所示,其中俯视图是一个腰长为2的等腰直角三角形,侧视图是一个直角边长为1的直角三角形,则该几何体外接球的体积是( )| A. | 36π | B. | 9π | C. | $\frac{9}{2}π$ | D. | $\frac{27}{5}π$ |
7.设直线l过双曲线C的一个焦点,且与C的一条对称轴垂直,l与C交于A,B两点,|AB|为C的实轴长的2倍,则C的离心率为( )
| A. | $\sqrt{3}$ | B. | $\sqrt{2}$ | C. | 2 | D. | 3 |
14.复数$z=\frac{i}{1-i}$的共轭复数的模为( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | 1 | D. | 2 |
11.若集合A={0,1,2,4},B={1,2,3},则A∩B=( )
| A. | {0,1,2,3,4} | B. | {0,1} | C. | {0,1,4} | D. | {1,2} |
8.椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{2}$=1(a>0)的长轴长为4,则C的离心率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\sqrt{2}$ |
 如图,四棱锥P-ABCD中,AD∥BC,$AB=BC=\frac{1}{2}AD$,E,F,H分别为线段AD,PC,CD的中点,AC与BE交于O点,G是线段OF上一点.
如图,四棱锥P-ABCD中,AD∥BC,$AB=BC=\frac{1}{2}AD$,E,F,H分别为线段AD,PC,CD的中点,AC与BE交于O点,G是线段OF上一点.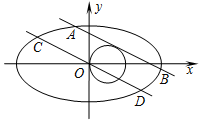 已知椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{{\sqrt{3}}}{2}$,且过点$({2,\sqrt{3}}))$,直线l1:y=kx+m(m>0)与圆C2:(x-1)2+y2=1相切且与椭圆C1交于A,B两点.
已知椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{{\sqrt{3}}}{2}$,且过点$({2,\sqrt{3}}))$,直线l1:y=kx+m(m>0)与圆C2:(x-1)2+y2=1相切且与椭圆C1交于A,B两点.