题目内容
下面几个命题中,假命题是( )
| A、“若a≤b,则2a≤2b-1”的否命题 |
| B、“?a∈(0,+∞),函数y=ax在定义域内单调递增”的否定 |
| C、“π是函数y=sinx的一个周期”或“2π是函数y=sin2x的一个周期” |
| D、“x2+y2=0”是“xy=0”的必要条件. |
考点:命题的真假判断与应用
专题:简易逻辑
分析:A.利用否命题的意义即可判断出;
B.利用指数函数的单调性即可得出;
C.利用正弦函数的单调性和“或命题”的意义即可判断出;
D.利用实数的性质和充分必要条件即可判断出.
B.利用指数函数的单调性即可得出;
C.利用正弦函数的单调性和“或命题”的意义即可判断出;
D.利用实数的性质和充分必要条件即可判断出.
解答:
解:A.“若a≤b,则2a≤2b-1”的否命题是“若a>b,则2a>2b-1”,是真命题;
B.“?a∈(0,+∞),函数y=ax在定义域内单调递增”的否定为“?a∈(0,+∞),函数y=ax在定义域内不单调递增”,正确,例如a=
时,函数y=(
)x在R上单调递减;
C.“π是函数y=sinx的一个周期”不正确,“2π是函数y=sin2x的一个周期”正确,
可知:“π是函数y=sinx的一个周期”或“2π是函数y=sin2x的一个周期”正确.
D.“x2+y2=0”⇒“xy=0”,反之不成立,因此“x2+y2=0”是“xy=0”的充分不必要条件,因此不正确.
综上可知:只有D是错误.
故选:D.
B.“?a∈(0,+∞),函数y=ax在定义域内单调递增”的否定为“?a∈(0,+∞),函数y=ax在定义域内不单调递增”,正确,例如a=
| 1 |
| 2 |
| 1 |
| 2 |
C.“π是函数y=sinx的一个周期”不正确,“2π是函数y=sin2x的一个周期”正确,
可知:“π是函数y=sinx的一个周期”或“2π是函数y=sin2x的一个周期”正确.
D.“x2+y2=0”⇒“xy=0”,反之不成立,因此“x2+y2=0”是“xy=0”的充分不必要条件,因此不正确.
综上可知:只有D是错误.
故选:D.
点评:本题考查了指数函数的单调性、正弦函数的单调性、简易逻辑的有关知识,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知正数x、y满足
,则z=(
)x•4-y的最小值为( )
|
| 1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
下列关于极限的计算,错误的是( )
A、
| ||||||||||||||||||||
B、
| ||||||||||||||||||||
C、
| ||||||||||||||||||||
D、已知an=
|
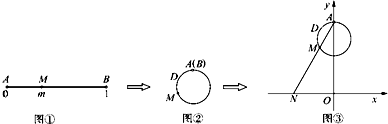 如图展示了一个由区间(0,1)到实数集R的映射过程:区间(0,1)中的实数m对应数轴上的点M,如图①;将线段AB围成一个圆,使两端点A、B恰好重合,如图②;再将这个圆放在平面直角坐标系中,使其圆心在y轴上,点A的坐标为(0,1),在图形变化过程中,图①中线段AM的长度对应于图③中的弧ADM的长度,如图③.图③中直线AM与x轴交于点N(n,0),则m的象就是n,记作f(m)=n.
如图展示了一个由区间(0,1)到实数集R的映射过程:区间(0,1)中的实数m对应数轴上的点M,如图①;将线段AB围成一个圆,使两端点A、B恰好重合,如图②;再将这个圆放在平面直角坐标系中,使其圆心在y轴上,点A的坐标为(0,1),在图形变化过程中,图①中线段AM的长度对应于图③中的弧ADM的长度,如图③.图③中直线AM与x轴交于点N(n,0),则m的象就是n,记作f(m)=n.