Question

若方程

3

sinx+cosx=a在[0，π]上有两个不同的实数解，则a的取值范围为

 

_．

Answer 1

考点：两角和与差的正弦函数

专题：计算题,函数的性质及应用,三角函数的图像与性质

分析：化已知问题为y=sin（x+

π

6

）在x∈[0，π]的图象与y=

a

2

的交点问题，数形结合可得．

解答： 解：方程

3

sinx+cosx=a可化为2sin（x+

π

6

）=a，
可化为sin（x+

π

6

）=

a

2

，
作出函数y=sin（x+

π

6

）在x∈[0，2π]的图象，

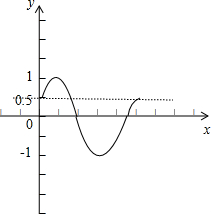
由图可知，当

1

2

≤

a

2

＜1，即1≤a＜2时，函数图象在[0，π]有两个不同的交点，
故方程

3

sinx+cosx=a在[0，π]上有两个不同的实数解，
故答案为：[1，2）．

点评：本题考查两角和与差的三角函数，数形结合是解决问题的关键，属于中档题．