题目内容

已知△ABC的内角A、B、C所对应边分别为a、b、c，若3a2+2ab+3b2-3c2=0，则sinC=
 
．
考点：余弦定理
专题：解三角形
分析：根据题意，由已知得a2+b2-c2=-
2
3
ab，由余弦定理求出cosC，即可求出sinC．
解答： 解：在△ABC中，∵3a2+2ab+3b2-3c2=0，
∴a2+b2-c2=-
2
3
ab；
又由余弦定理得，
cosC=
a2+b2-c2
2ab
=
-
2
3
ab
2ab
=-
1
3
，
∴sinC=
1-cos2C
=
1-(-
1
3
)2
=
2
2
3
．
故答案为：
2
2
3
．
点评：本题考查了解三角形的有关知识，解题时应灵活应用余弦定理解答问题，是基础题．
练习册系列答案
相关题目
动圆C的方程为x2+y2-2ax-4ay+
9
2
a2=0，是否存在定直线l它与动圆C总相切？并说明理由．
已知等差数列{an}的各项均为正数，且Sn=
1
a1a2
+
1
a2a3
+…+
1
anan+1
，S2=
2
3
，S3=
3
4
．设[x]表示不大于x的最大整数（如[2.10]=2，[0.9]=0）．
（1）试求数列{an}的通项；
（2）求T=[log21]+[log22]+[log23]+…+[log2（2 an-1）]+[log2（2 an）]关于n的表达式．
设
1
2
＜（
1
2
）b＜（
1
2
）a＜1，比较aa与ab与ba的大小．
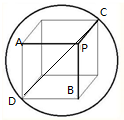如图，已知球O，球面上有四点P、A、B、C，且PC、PA、PB两两垂直，PC=5，PA=3，PB=4，若过C点的直径为CD，求二面角P-CD-A的大小．
设函数f（x）=sin（ωx+φ），A＞0，ω＞0，若f（x）在区间[
π
6
，
π
2
]上具有单调性，且f（
π
2
）=f（
2π
3
）=-f（
π
6
），则f（x）的最小正周期为
 
．
对a，b∈R，定义：max（a，b）=
 a    (a≥b)    
 b (a＜b)
，则函数f（x）=max（6x-6，-x+8）（x∈R）的最小值为
 
．
已知集合A={x|x＞1}，B={x|2m-1≤x≤m+3}，若B⊆A，则m的取值范围是
 
．
若函数f（x）=
x2+(a+1)x+a
x
为奇函数，则实数a=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网