题目内容
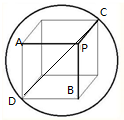 如图,已知球O,球面上有四点P、A、B、C,且PC、PA、PB两两垂直,PC=5,PA=3,PB=4,若过C点的直径为CD,求二面角P-CD-A的大小.
如图,已知球O,球面上有四点P、A、B、C,且PC、PA、PB两两垂直,PC=5,PA=3,PB=4,若过C点的直径为CD,求二面角P-CD-A的大小.考点:用空间向量求平面间的夹角,二面角的平面角及求法
专题:空间角,空间向量及应用
分析:由已知得A、B、C、D、P是长方体ODBE-FAPC上的五个顶点,以O为原点,OD为x轴,以OE为y轴,以OF为z轴,建立空间直角坐标系,利用向量法能求出二面角P-CD-A的平面角.
解答:
解: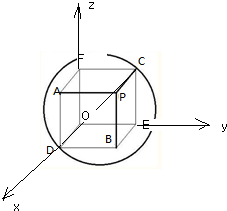 如图,球O的球面上有四点P、A、B、C,
如图,球O的球面上有四点P、A、B、C,
且PC、PA、PB两两垂直,PC=5,PA=3,PB=4,
∴A、B、C、D、P是长方体ODBE-FAPC上的五个顶点,
以O为原点,OD为x轴,以OE为y轴,以OF为z轴,
建立空间直角坐标系,
P(5,3,4),D(5,0,0),C(0,3,4),A(5,0,4),
=(-5,3,4),
=(0,3,4),
=(0,0,4),
设平面PCD的法向量
=(x,y,z),
则
,
取y=4,得
=(0,4,-3),
设平面CDA的法向量
=(a,b,c),
则
,
取a=3,得
=(3,5,0),
设二面角P-CD-A的平面角为θ,
cosθ=|cos<
,
>|=|
|=
.
 如图,球O的球面上有四点P、A、B、C,
如图,球O的球面上有四点P、A、B、C,且PC、PA、PB两两垂直,PC=5,PA=3,PB=4,
∴A、B、C、D、P是长方体ODBE-FAPC上的五个顶点,
以O为原点,OD为x轴,以OE为y轴,以OF为z轴,
建立空间直角坐标系,
P(5,3,4),D(5,0,0),C(0,3,4),A(5,0,4),
| DC |
| DP |
| DA |
设平面PCD的法向量
| n |
则
|
取y=4,得
| n |
设平面CDA的法向量
| m |
则
|
取a=3,得
| m |
设二面角P-CD-A的平面角为θ,
cosθ=|cos<
| m |
| n |
| 20 | ||||
|
2
| ||
| 17 |
点评:本题考查二面角的余弦值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
设a=
dx,则二项式(ax-
)8的展开式中x2项的系数是( )
| ∫ | e e-1 |
| 1 |
| x |
| 1 | ||
|
| A、-1120 | B、1120 |
| C、-1792 | D、1792 |
已知Sn,Tn分别是数列{an},{bn}的前n项和,若
=n+1,则
=( )
| Sn |
| Tn |
| a15 |
| b15 |
| A、16 | B、29 | C、30 | D、31 |
已知1,a,b,c,4成等比数列,则实数b为( )
| A、4 | B、-2 | C、±2 | D、2 |