题目内容
已知f(x)=log3(2x-3x2).
(1)求f(x)的值域;
(2)求f(x)的单调递增区间.
(1)求f(x)的值域;
(2)求f(x)的单调递增区间.
考点:对数函数的图像与性质
专题:函数的性质及应用
分析:(1)求出定义域为:(0,
),设u(x)=2x-3x2,x∈(0,
),求解得出0<u(x)≤
,即可求解值域.
(2)利用复合函数的单调性求解即可.
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
(2)利用复合函数的单调性求解即可.
解答:
解:(1)∵f(x)=log3(2x-3x2).
∴定义域为:(0,
),
设u(x)=2x-3x2,x∈(0,
),
对称轴x=
,∴u(
)=
-
=
,
故0<u(x)≤
,
∴f(x)≤log3
=-1,
故值域为:y∈(-∞,-1],
(2)根据复合函数的单调性得出:
f(x)的单调递增区间为:(0,
),
∴定义域为:(0,
| 2 |
| 3 |
设u(x)=2x-3x2,x∈(0,
| 2 |
| 3 |
对称轴x=
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
故0<u(x)≤
| 1 |
| 3 |
∴f(x)≤log3
| 1 |
| 3 |
故值域为:y∈(-∞,-1],
(2)根据复合函数的单调性得出:
f(x)的单调递增区间为:(0,
| 1 |
| 3 |
点评:本题考查了复合函数的性质,运用对数,二次函数性质,注意定义域的限制.

练习册系列答案
相关题目
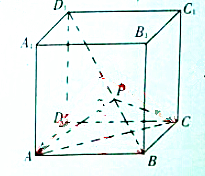
如图,已知正方体ABCD-A1B1C1D1棱长为1,点P在线段BD1上,当∠APC最大时,三棱锥P-ABC的体积为( )

A、
| ||
B、
| ||
C、
| ||
D、
|