题目内容
已知点A（4，-2）和点B（2，4），则线段AB的垂直平分线方程为 ．
考点：直线的一般式方程与直线的垂直关系
专题：直线与圆
分析：由中点公式和斜率公式以及垂直关系可得直线的斜率和过的定点，可得点斜式方程，化为一般式即可．
解答：
解：∵点A（4，-2）和点B（2，4），
∴AB的中点为（3，1），
由斜率公式可得kAB=
=-3，
∴由垂直关系可得所求直线的斜率为
，
∴所求直线的方程为y-1=
（x-3）
化为一般式可得x-3y=0
故答案为：x-3y=0
∴AB的中点为（3，1），
由斜率公式可得kAB=
| -2-4 |
| 4-2 |
∴由垂直关系可得所求直线的斜率为
| 1 |
| 3 |
∴所求直线的方程为y-1=
| 1 |
| 3 |
化为一般式可得x-3y=0
故答案为：x-3y=0
点评：本题考查直线的一般式方程和垂直关系，属基础题．
练习册系列答案
相关题目
设a=log3π，b=log2
，c=log3
，则（ ）
| 3 |
| 2 |
| A、a＞c＞b |
| B、b＞c＞a |
| C、b＞a＞c |
| D、a＞b＞c |
若实数x，y满足
，则|x|+y的取值范围为（ ）
|
| A、[2，3] |
| B、[0，3] |
| C、[-1，2] |
| D、[-1，3] |
如图，阴影部分的面积是（ ）
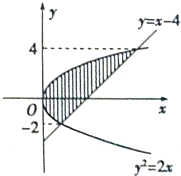
| A、16 | B、18 | C、20 | D、22 |
如图所示，在菱形ABCD中，∠BAD=120°，则下列说法中错误说法的个数是（ ）下列四个命题中，其中真命题为（ ）
| A、若函数y=f（x）在一点的导数值为0，则函数y=f（x）在这点处取极值 | ||||
B、命题“若α=
| ||||
| C、已知a，b是实数，则“a＞0且b＞0”是“a+b＞0且ab＞0”的充分不必要条件 | ||||
D、函数f（x）=
|
已知函数f（x）=
，若对任意xx≠x2，都有
＜0成立，则a的取值范围是（ ）
|
| f(x1)-f(x ) |
| x1-x2 |
A、（0，
| ||
B、（
| ||
| C、（1，2） | ||
| D、（-1，2） |