题目内容
如图所示，在菱形ABCD中，∠BAD=120°，则下列说法中错误说法的个数是（ ）①图中所标出的向量中与
| AB |
| AB |
②图中所标出的向量与
| AB |
| AB |
③
| BD |
| DA |
| 3 |
④
| CB |
| DA |
| A、4 | B、3 | C、1 | D、0 |
考点：命题的真假判断与应用
专题：平面向量及应用,简易逻辑
分析：①利用向量相等与菱形的性质即可判断出正误；
②利用菱形的性质、模相等的定义即可判断出正误；
③利用菱形的性质、直角三角形的边角关系即可判断出正误．
④利用向量共线定理即可判断出
与
共线，即可判断出正误．
②利用菱形的性质、模相等的定义即可判断出正误；
③利用菱形的性质、直角三角形的边角关系即可判断出正误．
④利用向量共线定理即可判断出
| CB |
| DA |
解答：
解：①图中所标出的向量中与
相等的向量只有1个
，（不含
本身），正确；
②图中所标出的向量与
的模相等的向量有4个
，
，
，
（不含
本身），正确；
③利用菱形的性质、直角三角形的边角关系可得：
的长度恰为
长度的
倍，正确．
④
与
共线，因此不正确．
因此说法中错误说法的个数是1．
故选：C．
| AB |
| DA |
| AB |
②图中所标出的向量与
| AB |
| DA |
| DC |
| CA |
| CB |
| AB |
③利用菱形的性质、直角三角形的边角关系可得：
| BD |
| DA |
| 3 |
④
| CB |
| DA |
因此说法中错误说法的个数是1．
故选：C．
点评：本题考查了向量相等、菱形的性质、模相等的定义、直角三角形的边角关系、向量共线定理、简易逻辑的判定，考查了推理能力，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
命题“存在x∈R，使2x+x2≤1”的否定是（ ）
| A、对任意x∈R，有2x+x2＞1 |
| B、对任意x∈R，有2x+x2≤1 |
| C、存在x∈R，使2x+x2＞1 |
| D、不存在x∈R，使2x+x2≤1 |
已知直线ax+by=0，从集合{1，2，3，4}中任选两个数分别作为a，b，则得到的不同直线有（ ）
| A、10条 | B、12条 |
| C、18条 | D、20条 |
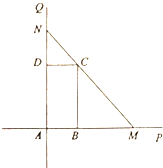如图，互相垂直的两条公路AP，AQ旁有一矩形花园ABCD，现欲将其扩建成一个更大的三角形花园AMN，要求点M在射线AP上，点N在射线AQ上，且直线MN过点C，其中AB=10m，AD=20m，记三角形花园AMN的面积为S，