题目内容

如图，阴影部分的面积是（　　）
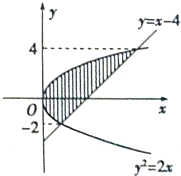
A、16B、18C、20D、22
考点：定积分在求面积中的应用
专题：导数的综合应用
分析：利用定积分的几何意义，首先表示阴影部分的面积，然后计算．
解答： 解：由已知，直线与抛物线的交点坐标分别为（2，-2），（8，4），
所以阴影部分的面积为：
∫
4
-2
(y+4-
y2
2
)dy=（
1
2
y2+4y-
1
6
y3）|
 
4
-2
=18；
故选B．
点评：本题考查了利用定积分的几何意义求曲边梯形的面积；关键是正确利用定积分表示曲边梯形的面积，然后再去计算．
练习册系列答案
相关题目
已知直线y=
1
2
x与抛物线y2=2px（p＞0）交于O，A两点（F为抛物线的焦点，O为坐标原点），若|AF|=17，求OA的垂直平分线的方程．
设x，y，z∈（0，1）．求证x（1-y）+y（1-z）+z（1-x）＜1．
若函数y=a-bsin（3x+
π
6
）的最大值为
3
2
，最小值为-
1
2
，则a=
 
，b=
 
．
已知点A（4，-2）和点B（2，4），则线段AB的垂直平分线方程为
 
．
已知数列{an}满足：a1=1，an+1-2an=n+1，n∈N*
（1）求证：数列{an+n+2}是等比数列；
（2）若数列{an}的前n项和为Sn，求an和Sn．
已知直线ax+by=0，从集合{1，2，3，4}中任选两个数分别作为a，b，则得到的不同直线有（　　）
A、10条B、12条
C、18条D、20条
已知θ∈(-
π
2
，π)，若函数f（x）=cos（ωx+
π
6
+θ）是周期为π的奇函数，则函数y=sin（ωx+θ）的单调增区间为（　　）
A、[kπ-
5π
12
，kπ+
π
6
]（k∈Z）
B、[kπ-
π
6
，kπ+
π
3
]（k∈Z）
C、[kπ-
5π
12
，kπ+
π
12
]（k∈Z）
D、[kπ-
π
3
，kπ+
π
6
]（k∈Z）
已知函数f（x）=Asin（ωx+φ），其中ω＞0．
（1）当A=ω=2，φ=
π
6
时，函数g（x）=f（x）-m在[0，
π
2
]上有两个零点，求m的范围；
（2）当A=1，φ=
π
6
时，若函数f（x）图象的相邻两条对称轴之间的距离等于
π
2
，求函数f（x）的解析式，并求最小正实数n，使得函数f（x）的图象向左平移n个单位所对应的函数是奇函数．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网