题目内容
若实数x,y满足
,则|x|+y的取值范围为( )
|
| A、[2,3] |
| B、[0,3] |
| C、[-1,2] |
| D、[-1,3] |
考点:简单线性规划
专题:不等式的解法及应用
分析:由约束条件作出可行域,对x≥0和x≤0分类,当x≥0时,目标函数化为z=x+y,化为斜截式得y=-x+z,可行域为
阴影部分中y轴及其右侧部分,目标函数取得最大值的最优解的坐标为(2,0),取得最小值的最优解的坐标为(0,-1),当x≤0时目标函数化为z=-x+y,化为斜截式得y=x+z,目标函数取得最大值的最优解的坐标为(-1,2),取得最小值的最优解的坐标为(0,-1).然后分别求出最大值和最小值取并集得答案.
阴影部分中y轴及其右侧部分,目标函数取得最大值的最优解的坐标为(2,0),取得最小值的最优解的坐标为(0,-1),当x≤0时目标函数化为z=-x+y,化为斜截式得y=x+z,目标函数取得最大值的最优解的坐标为(-1,2),取得最小值的最优解的坐标为(0,-1).然后分别求出最大值和最小值取并集得答案.
解答:
解:由约束条件
作出可行域如图,
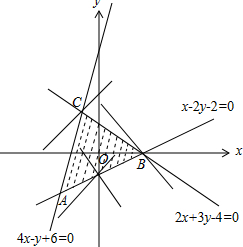
令z=|x|+y,当x>0时,z=x+y,化为斜截式,得y=-x+z,
由图可知,当直线y=-x+z过B(2,0)时,直线在y轴上的截距最大,z最大,为z=2.
当直线y=-x+z过(0,-1)时,直线在y轴上的截距最小,z最小,为z=-1.
当x<0时,z=-x+y,化为斜截式,得y=x+z,
由图可知,当直线过C(-1,2)时,直线在y轴上的截距最大,为z=-(-1)+2=3.
当直线过(0,-1)时,直线在y轴上的截距最小,为z=-1.
综上,|x|+y的取值范围为[-1,3].
故选:D.
|

令z=|x|+y,当x>0时,z=x+y,化为斜截式,得y=-x+z,
由图可知,当直线y=-x+z过B(2,0)时,直线在y轴上的截距最大,z最大,为z=2.
当直线y=-x+z过(0,-1)时,直线在y轴上的截距最小,z最小,为z=-1.
当x<0时,z=-x+y,化为斜截式,得y=x+z,
由图可知,当直线过C(-1,2)时,直线在y轴上的截距最大,为z=-(-1)+2=3.
当直线过(0,-1)时,直线在y轴上的截距最小,为z=-1.
综上,|x|+y的取值范围为[-1,3].
故选:D.
点评:本题考查了简单的线性规划,考查了数形结合的解题思想方法,考查了分类讨论的数学思想方法,是中档题.

练习册系列答案
相关题目
函数y=x+
(x>0))的最小值为6,则正数a的值为( )
| a |
| x |
| A、1 | B、4 | C、9 | D、16 |
已知a,b∈R,若a>b,则下列不等式成立的是( )
| A、lga>lgb | ||||||
| B、0.5a>0.5b | ||||||
C、a
| ||||||
D、
|
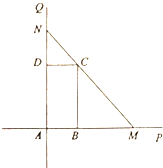 如图,互相垂直的两条公路AP,AQ旁有一矩形花园ABCD,现欲将其扩建成一个更大的三角形花园AMN,要求点M在射线AP上,点N在射线AQ上,且直线MN过点C,其中AB=10m,AD=20m,记三角形花园AMN的面积为S,
如图,互相垂直的两条公路AP,AQ旁有一矩形花园ABCD,现欲将其扩建成一个更大的三角形花园AMN,要求点M在射线AP上,点N在射线AQ上,且直线MN过点C,其中AB=10m,AD=20m,记三角形花园AMN的面积为S,