题目内容
已知集合M=|(x,y)|y=f(x)|,若对任意P1(x1,y1)∈M,均不存在P2(x2,y2)∈M,使得x1x2+y1y2=0成立,则称集合M为“好集合”,给出下列五个集合:
①M={(x,y)|y=
};
②M={(x,y)|y=lnx};
③M={(x,y)|y=
x2+1};
④M={(x,y)|(x-2)2+y2=1};
其中所有“好集合”的序号是 .(写出所有正确答案的序号)
①M={(x,y)|y=
| 1 |
| x |
②M={(x,y)|y=lnx};
③M={(x,y)|y=
| 1 |
| 4 |
④M={(x,y)|(x-2)2+y2=1};
其中所有“好集合”的序号是
考点:命题的真假判断与应用
专题:函数的性质及应用,简易逻辑
分析:对于①,利用x1x2+
=0无实数解,判断其正误即可;对于②③,取一个特殊点即能说明不满足“好集合”定义;
画图后求出过原点的圆的两条切线方程,说明集合中任取一点,P1(x1,y1)∈M,均不存在P2(x2,y2)∈M,使得x1x2+y1y2=0成立.
| 1 |
| x1x2 |
画图后求出过原点的圆的两条切线方程,说明集合中任取一点,P1(x1,y1)∈M,均不存在P2(x2,y2)∈M,使得x1x2+y1y2=0成立.
解答:
解:对于①,x1x2+
=0无实数解,因此①是“好集合”;
对于②,取点(
,-1),存在点(e,1)∈M,使得
•e+(-1)•1=0,因此②不是“好集合”;
对于③,取点(-2,2),存在点(2,2)∈M,使得-2×2+2×2=0,因此③不是“好集合”;
对于④,集合M中点的轨迹为以(2,0)为圆心,以1为半径的圆,如图,
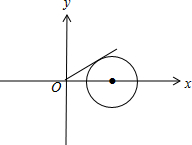
设过原点的一条切线方程为kx-y=0,由(2,0)到切线的距离等于1得:
=1,解得:k=±
.
∴集合M中两点间的最大夹角为
,即在集合中任取一点,P1(x1,y1)∈M,均不存在P2(x2,y2)∈M,使得x1x2+y1y2=0成立,因此①是“好集合”.
故答案为:①④.
| 1 |
| x1x2 |
对于②,取点(
| 1 |
| e |
| 1 |
| e |
对于③,取点(-2,2),存在点(2,2)∈M,使得-2×2+2×2=0,因此③不是“好集合”;
对于④,集合M中点的轨迹为以(2,0)为圆心,以1为半径的圆,如图,

设过原点的一条切线方程为kx-y=0,由(2,0)到切线的距离等于1得:
| |2k| | ||
|
| ||
| 3 |
∴集合M中两点间的最大夹角为
| π |
| 3 |
故答案为:①④.
点评:本题考查了命题真假的判断与应用,考查了元素与集合的关系,考查了数形结合的思想,解答的关键是对新定义的理解,是中档题.

练习册系列答案
相关题目
已知函数f(x)=
若f(f(0))≥a2-1,则实数a的取值范围为( )
|
| A、[3,4] |
| B、[2,3] |
| C、[1,2] |
| D、[-1,2] |
若p是真命题,q是假命题,以下四个命题:p且q,p或q,非p,非q,其中假命题的个数是( )
| A、1 | B、2 | C、3 | D、4 |
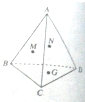 如图,已知A为平面BCD外一点,M,N,G分别是△ABC、△ABD、△BCD的重心,求证:平面MNG∥平面ACD.
如图,已知A为平面BCD外一点,M,N,G分别是△ABC、△ABD、△BCD的重心,求证:平面MNG∥平面ACD.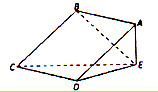 如图所示四棱锥E-ABCD中,四边形ABCD为正方形,AE⊥平面CDB,且AR=3,
如图所示四棱锥E-ABCD中,四边形ABCD为正方形,AE⊥平面CDB,且AR=3,