题目内容
某企业在第1年初购买一台价值为120万元的设备M,M的价值在使用过程中逐年减少,从第2年到第6年,每年初M的价值比上年初减少10万元;从第7年开始,每年初M的价值为上年初的75%.
(1)求第n年初M的价值an的表达式;
(2)设An=
若An大于80万元,则M继续使用,否则须在第n年初对M更新,证明:第6年初仍可对M继续使用.
(1)求第n年初M的价值an的表达式;
(2)设An=
| a1+a2+…+an |
| n |
考点:数列的应用
专题:等差数列与等比数列
分析:(1)当n≤6时,an=120-10(n-1)=130-10n,当n≥6时,数列{an}是以a6为首项,公比为
的等比数列,
又a6=70,由此能求出第n年初M的价值an的表达式.
(2)设Sn表示数列{an}的前n项和,当1≤n≤6时,Sn=120n-5n(n-1),An=120-5(n-1)=125-5n,由此能求出第6年初仍可对M继续使用.
| 3 |
| 4 |
又a6=70,由此能求出第n年初M的价值an的表达式.
(2)设Sn表示数列{an}的前n项和,当1≤n≤6时,Sn=120n-5n(n-1),An=120-5(n-1)=125-5n,由此能求出第6年初仍可对M继续使用.
解答:
解:(1)当n≤6时,数列{an}是首项为120,公差为-10的等差数列.
an=120-10(n-1)=130-10n,
当n≥6时,数列{an}是以a6为首项,公比为
的等比数列,
又a6=70,所以an=70×(
)n-6,
因此,第n年初M的价值an的表达式为an=
.
(2)设Sn表示数列{an}的前n项和,
由等差数列的求和公式得
当1≤n≤6时,Sn=120n-5n(n-1),
An=120-5(n-1)=125-5n,
A6=125-5×6=95>80,
所以,第6年初仍可对M继续使用.
an=120-10(n-1)=130-10n,
当n≥6时,数列{an}是以a6为首项,公比为
| 3 |
| 4 |
又a6=70,所以an=70×(
| 3 |
| 4 |
因此,第n年初M的价值an的表达式为an=
|
(2)设Sn表示数列{an}的前n项和,
由等差数列的求和公式得
当1≤n≤6时,Sn=120n-5n(n-1),
An=120-5(n-1)=125-5n,
A6=125-5×6=95>80,
所以,第6年初仍可对M继续使用.
点评:本题考查数列有生产生活中的具体应用,是中档题,解题时要认真审题,注意数列性质的合理运用.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案
相关题目
下表是降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对应数据,根据表中提供的数据,求出y关于x的线性回归方程为
=0.7x+0.35,那么表中m值为( )
 |
| y |
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | m | 4 | 4.5 |
| A、4 | B、3.15 | C、4.5 | D、3 |
下列四个命题中,正确的是( )
| A、人的年龄与其拥有的财富之间具有相关关系 | ||||
| B、从独立性检验可知,在犯错误的概率不超过1%的情况下,有把握认为吃地沟油与患胃肠癌有关系时,我们说某一个人吃地沟油,那么他有99%的可能患胃肠癌 | ||||
| C、从独立性检验可知,在犯错误的概率不超过5%的情况下,有把握认为吃地沟油与患胃肠癌有关系时,是指有少于5%的可能性使得推断吃地沟油与患胃肠癌有关系出现错误 | ||||
D、已知一系列样本点(xi,yi)(i=1,2,3,…,n)的回归直线方程为
|
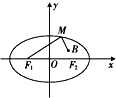 如图,已知椭圆
如图,已知椭圆