题目内容

已知函数f（x）=
2x+1，x≤0
x2+ax，x＞0
若f（f（0））≥a2-1，则实数a的取值范围为（　　）
A、[3，4]
B、[2，3]
C、[1，2]
D、[-1，2]
考点：分段函数的应用
专题：函数的性质及应用
分析：先求f（0）=2×0+1=1，代入可得f（f（0））=f（1）=1+a，则f（f（0））≥a2-1等价化为1+a≥a2-1，解此二次不等式即可得到答案．
解答： 解：∵f（0）=2×0+1=1，
∴f（f（0））=f（1）=1+a，
则f（f（0））≥a2-1等价化为1+a≥a2-1，
化简解得-1≤a≤2．
故选：D
点评：本题考查了分段函数的解析式，分段函数的取值问题．主要考查了根据自变量的值求函数的函数值，解题的关键是判断该用哪段解析式进行求解．
练习册系列答案
相关题目
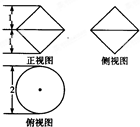某几何体的三视图如图所示，则该几何体的体积为（　　）
A、
2
π
B、2
2
π
C、
π
3
D、
2π
3
画出函数y=
4(x2+2x+1)2
+
3(x-1)3
的图象．
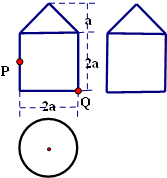一个几何体的三视图及部分度量值如图所示，其中，正视图与侧视图都是由一个正方形和一个等腰三角形组成，俯视图是一个圆．
（1）判断该几何体的结构特征，并求其表面积；
（2）如果正视图中的点P是其所在线段的中点，点Q是其所在正方形的顶点，试求：在原几何体的侧面上，从P点到Q点的最短路径的长．
三角形的一边长为
39
，这条边所对的角为60°，另两边之比为3：4，则这个三角形的面积为
 
．
某展览馆22天中每天进馆参观的人数如下：
180158170185189180184185140179192
185190165182170190183175180185148
计算参观人数的中位数、众数、平均数．
已知集合M=|（x，y）|y=f（x）|，若对任意P1（x1，y1）∈M，均不存在P2（x2，y2）∈M，使得x1x2+y1y2=0成立，则称集合M为“好集合”，给出下列五个集合：
①M={（x，y）|y=
1
x
 }；  
②M={（x，y）|y=lnx}；  
③M={（x，y）|y=
1
4
 x2+1}；
④M={（x，y）|（x-2）2+y2=1}；
其中所有“好集合”的序号是
 
．（写出所有正确答案的序号）
已知二次函数f（x）=2x2+ax+b为偶函数，g（x）=（
3
-1）x+m，h（x）=c（x+1）2（c≠2），关于x的方程f（x）=h（x）有且仅有一根
1
2
．
（Ⅰ）求a，b，c的值；
（Ⅱ）若对任意的x∈[-1，1]，
f(x)
≤g（|x|）恒成立，求实数m的取值范围；
（Ⅲ）令φ（x）=
f(x)
+
f(1-x)
，若存在x1，x2∈[0，1]使得|φ（x1）-φ（x2）|≥g（m），求实数m的取值范围．
已知不等式组
x2-x-2＞0
2x2+(5+2k)x+5k＜0.

（1）当k=0时，求不等式组的解区间；
（2）若不等式组的整数解只有一个-2，求实数k的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网