Question

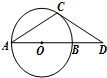（几何证明选讲选做题）如图，已知点D在圆O直径AB的延长线上，过D作圆O的切线，切点为C．若CD=

3

，BD=1，则圆O的面积为

 

．
（坐标系与参数方程选做题）在直角坐标系xOy中，曲线l的参数方程为

x=t y=3+t.

(t为参数）；以原点O为极点，以x轴的正半轴为极轴建立极坐标系ρOθ，则曲线l的极坐标方程为

 

．

Answer 1

考点：简单曲线的极坐标方程

专题：直线与圆,立体几何,坐标系和参数方程

分析：①如图所示，连接OC，利用切线的性质可得：OC⊥CD．设⊙O的半径为r，利用勾股定理可得：OC²+CD²=OD²，即r2+(

3

)2=(r+1)2，解得r即可．即可得到⊙O的面积S．
②由曲线l的参数方程为

x=t y=3+t.

(t为参数），消去参数t可得：y-x=3，把x=ρcosθ，y=ρsinθ代入上式即可得出．

解答： 解：①如图所示，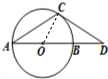
连接OC，∵CD是⊙O的切线，
∴OC⊥CD．
设⊙O的半径为r，
在Rt△OCD中，OC²+CD²=OD²，
∴r2+(

3

)2=(r+1)2，化为3=2r+1，解得r=1．
∴⊙O的面积S=π×1²=π．
②由曲线l的参数方程为

x=t y=3+t.

(t为参数），消去参数t可得：y-x=3；
把x=ρcosθ，y=ρsinθ代入上式可得ρsinθ-ρcosθ=3．
故答案分别为：π，ρ（sinθ-cosθ）=3．

点评：本题考查了圆的切线的性质、勾股定理、直线的参数方程化为极坐标方程，属于基础题．