题目内容
已知直角三角形ABC，其中∠ABC=60°，∠C=90°，AB=2，求△ABC绕斜边AB旋转一周所形成的几何体的表面积和体积．考点：组合几何体的面积、体积问题
专题：计算题,空间位置关系与距离
分析：以斜边AB为轴旋转一周，所得旋转体的形状是AB边的高CO为底面半径的两个圆锥组成的组合体，几何体的表面积是两个圆锥的侧面积之和，分别计算出两个圆锥的母线长，代入圆锥侧面积公式；即可求出旋转体的表面积；计算出底面半径及两个圆锥高的和，代入圆锥体积公式，即可求出旋转体的体积．
解答：
解：如图以斜边AB为轴旋转一周，得旋转体是以AB边的高CO为底面半径的两个圆锥组成的组合体
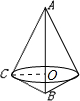∵AB=2，CB=1，∠B=60°
∴CB=sin30°•AB=1，CA=cos30°•AB=
，
CO=
=
，
故此旋转体的表面积，S=π×OC×AC+π×OC×BC=π×
×（
+1）=
π．
故此旋转体的体积V=
•πr2•h=
•π•CO2•AB=
×π×
×2=
．
∵AB=2，CB=1，∠B=60°∴CB=sin30°•AB=1，CA=cos30°•AB=
| 3 |
CO=
| AC•CB |
| AB |
| ||
| 2 |
故此旋转体的表面积，S=π×OC×AC+π×OC×BC=π×
| ||
| 2 |
| 3 |
3+
| ||
| 2 |
故此旋转体的体积V=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 3 |
| 4 |
| π |
| 2 |
点评：本题考查旋转体的表面积与体积的求法，判断旋转体的形状，旋转半径以及母线长，求出几何体的高是解答问题的关键．
练习册系列答案
寒假大串联黄山书社系列答案
相关题目
在R上定义运算：对x、y∈R，有x⊕y=2x+y，如果a⊕（3b）=1，（ab＞0），则
⊕(
)的最小值是（ ）
| 1 |
| a |
| 1 |
| 3b |
| A、4 | ||
B、
| ||
| C、9 | ||
D、
|
流程如图所示，现输入如下四个函数，则可以输出的函数是（ ）
| A、f（x）=x2 | ||
B、f（x）=
| ||
| C、f（x）=lnx+2x-6 | ||
| D、f（x）=sinx |