题目内容
过点P（1，1）的直线将圆形区域{（x，y）|x2+y2≤9}分成两部分，使得两部分的面积相差最大，则该直线的方程是（ ）
| A、x+y-2=0 |
| B、y-1=0 |
| C、x-y=0 |
| D、x+3y-4=0 |
考点：直线与圆的位置关系
专题：直线与圆
分析：根据题意画出相应的图形，由题意得到当直线CD与过P的直径AB垂直时，将圆形区域分成两部分的面积相差最大，求出直径AB所在直线方程的斜率，确定出直线CD的斜率，确定出CD的方程，即为所求．
解答：
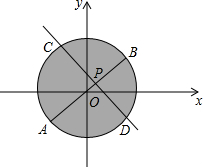解：根据题意画出图形，如图所示，
当直线CD与过P的直径AB垂直时，将圆形区域分成两部分的面积相差最大，
∵圆心O（0，0），P（1，1），
∴直径AB所在直线方程的斜率为
=1，
∴直线CD斜率为-1，方程为y-1=-（x-1），即x+y-2=0．
故选A
解：根据题意画出图形，如图所示，当直线CD与过P的直径AB垂直时，将圆形区域分成两部分的面积相差最大，
∵圆心O（0，0），P（1，1），
∴直径AB所在直线方程的斜率为
| 1-0 |
| 1-0 |
∴直线CD斜率为-1，方程为y-1=-（x-1），即x+y-2=0．
故选A
点评：此题考查了直线与圆的位置关系，根据题意得出直线CD与过P的直径AB垂直时，将圆形区域分成两部分的面积相差最大是解本题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
流程如图所示，现输入如下四个函数，则可以输出的函数是（ ）
| A、f（x）=x2 | ||
B、f（x）=
| ||
| C、f（x）=lnx+2x-6 | ||
| D、f（x）=sinx |
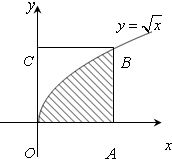在边长为1的正方形OABC中任取一点P，则点P恰好落在正方形与曲线y=| x |
A、
| ||
B、
| ||
C、
| ||
D、
|