题目内容
如图，已知E、F分别是矩形ABCD的边BC、CD的中点，EF与AC交于点G，若| AB |
| a |
| AD |
| b |
| a |
| b |
| AG |
考点：向量加减混合运算及其几何意义
专题：平面向量及应用
分析：如图所示，建立坐标系，B（a，0），D（0，b），E(a，
)，F(
，b)，C（a，b）．直线AC的方程为：y=
x，直线EF的方程为2bx+2ay-3ab=0．联立解得G的坐标，即可得出．
| b |
| 2 |
| a |
| 2 |
| b |
| a |
解答：
解：如图所示，建立坐标系，
B（a，0），D（0，b），E(a，
)，F(
，b)，C（a，b）．
直线AC的方程为：y=
x，
直线EF的方程为y-b=
(x-
)，化为2bx+2ay-3ab=0．
联立
，解得
．
∴
=(
a，
b)=
+
．
B（a，0），D（0，b），E(a，
| b |
| 2 |
| a |
| 2 |
直线AC的方程为：y=
| b |
| a |
直线EF的方程为y-b=
b-
| ||
|
| a |
| 2 |
联立
|
|
∴
| AG |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| a |
| 3 |
| 4 |
| b |
点评：本题考查了通过建立坐标系表示向量，属于基础题．
练习册系列答案
相关题目
已知定义在R上的函数f（x）满足下列三个条件：
①对任意的x∈R，都有f（x+4）=f（x）；
②对任意的0≤x1＜x2≤2，都有f（x1）＜f（x2）；
③y=f（x+2）的图象关于y轴对称，
则下列结论中，正确的是（ ）
①对任意的x∈R，都有f（x+4）=f（x）；
②对任意的0≤x1＜x2≤2，都有f（x1）＜f（x2）；
③y=f（x+2）的图象关于y轴对称，
则下列结论中，正确的是（ ）
| A、f（7）＜f（4.5）＜f（6.5） |
| B、f（7）＜f（6.5）＜f（4.5） |
| C、f（4.5）＜f（6.5）＜f（7） |
| D、f（4.5）＜f（7）＜f（6.5） |
设全集为R，函数f（x）=
的定义域为M，函数f（x）=ln（x2-4x）的定义域为N，则M∩N=（ ）
| 4-x2 |
| A、[-2，0） |
| B、（-∞，-2] |
| C、（4，+∞） |
| D、（-∞，0]∪（4，+∞） |
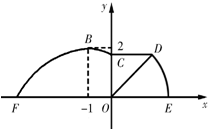如图，某市准备在道路EF的一侧修建一条运动比赛道，赛道的前一部分为曲线段FBC．该曲线段是函数y=Asin（ωx+
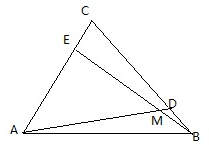如图，D、E分别为等边△ABC的边BC，AC上一点，BD=CE，∠CAD=45°，AD、BE交于M．
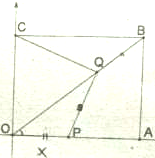如图，在矩形OABC中，O为原点，B点坐标为（8，6）．