题目内容
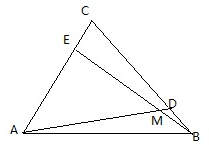如图，D、E分别为等边△ABC的边BC，AC上一点，BD=CE，∠CAD=45°，AD、BE交于M．（1）求∠AME的度数；
（2）求
| BM |
| AM |
考点：相似三角形的判定
专题：立体几何
分析：（1）由BD=CE，可得△ABD≌△BCE，进而∠DAB=∠EBC，由三角形外角等于不相邻两内角的和，可得∠AME=∠ABE+∠DAB=∠ABE+∠EBC=∠ABC=60°，
（2）过M点作AB的垂线，垂足为N，则∠DAB=15°，∠ABE=45°，则AM=
=（
+
）MN，BM=
=
MN，进而可得
的值．
（2）过M点作AB的垂线，垂足为N，则∠DAB=15°，∠ABE=45°，则AM=
| MN |
| sin15° |
| 6 |
| 2 |
| MN |
| sin45° |
| 2 |
| BM |
| AM |
解答：
解：（1）∵D、E分别为等边△ABC的边BC，AC上一点，BD=CE，
∴△ABD≌△BCE，
∴∠DAB=∠EBC，
∴∠AME=∠ABE+∠DAB=∠ABE+∠EBC=∠ABC=60°，
（2）过M点作AB的垂线，垂足为N，
∵∠CAD=45°，
∴∠DAB=15°，∠ABE=45°，
∴AM=
=（
+
）MN，BM=
=
MN，
∴
=
=
-
∴△ABD≌△BCE，
∴∠DAB=∠EBC，
∴∠AME=∠ABE+∠DAB=∠ABE+∠EBC=∠ABC=60°，
（2）过M点作AB的垂线，垂足为N，
∵∠CAD=45°，
∴∠DAB=15°，∠ABE=45°，
∴AM=
| MN |
| sin15° |
| 6 |
| 2 |
| MN |
| sin45° |
| 2 |
∴
| BM |
| AM |
| ||||
|
| ||
| 2 |
| 1 |
| 2 |
点评：本题考查的知识点是三角形全等的判定与性质，解三角形，难度不大，属于基础题．
练习册系列答案
习题精选系列答案
相关题目
在△ABC中，已知sinAcosB=sinC，那么△ABC一定是（ ）
| A、直角三角形 |
| B、等腰三角形 |
| C、等腰直角三角形 |
| D、正三角形 |
在区间[一π，π]内随机取两个数分别记为a，b，则使得函数f（x）=4x2+4ax-b2+π2有2个零点的概率为（ ）
A、
| ||
B、1一
| ||
C、
| ||
D、l-
|
如图，已知E、F分别是矩形ABCD的边BC、CD的中点，EF与AC交于点G，若