题目内容
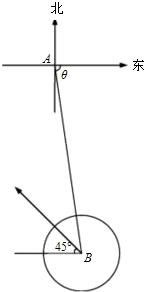 据气象台预报,一台风中心位于某沿海城市A东偏南θ(cosθ=
据气象台预报,一台风中心位于某沿海城市A东偏南θ(cosθ=
| ||
| 10 |
考点:解三角形的实际应用
专题:应用题,解三角形
分析:建立坐标系,设在时刻:t(h)台风中心B(x,y)的坐标进而可知此时台风侵袭的区域,根据题意可知其中r(t)=10t+60,若在t时,该城市A受到台风的侵袭,则有(0-x)2+(0-y)2≤(10t+60)2,进而可得关于t的一元二次不等式,求得t的范围,答案可得.
解答:
解:以A为原点,正东方向为x轴正向.
∵cosθ=
,∴sin(90°-θ)=
,
cos(90°-θ)=
,
在时刻:t(h)台风中心B(x,y)的坐标为
x=300×
-20×
t,y=-300×
+20×
t
令(x′,y′)是台风边缘线上一点,则此时台风侵袭的区域是(x′-x)2+(y′-y)2≤[r(t)]2,
其中r(t)=10t+60,
若在t时,该城市受到台风的侵袭,
则有(0-x)2+(0-y)2≤(10t+60)2,
即(300×
-20×
t)2+-300×
+20×
t)2≤(10t+60)2,
即t2-36t+288≤0,
解得12≤t≤24.
答:12小时后该城市开始受到台风气侵袭,受到台风的侵袭的时间有12小时.
∵cosθ=
| ||
| 10 |
| ||
| 10 |
cos(90°-θ)=
7
| ||
| 10 |
在时刻:t(h)台风中心B(x,y)的坐标为
x=300×
| ||
| 10 |
| ||
| 2 |
7
| ||
| 10 |
| ||
| 2 |
令(x′,y′)是台风边缘线上一点,则此时台风侵袭的区域是(x′-x)2+(y′-y)2≤[r(t)]2,
其中r(t)=10t+60,
若在t时,该城市受到台风的侵袭,
则有(0-x)2+(0-y)2≤(10t+60)2,
即(300×
| ||
| 10 |
| ||
| 2 |
7
| ||
| 10 |
| ||
| 2 |
即t2-36t+288≤0,
解得12≤t≤24.
答:12小时后该城市开始受到台风气侵袭,受到台风的侵袭的时间有12小时.
点评:本题主要考查了圆的方程的综合运用,考查了学生运用所学知识解决实际问题的能力,属于中档题.

练习册系列答案
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
若
=
+
则( )
| OC |
| 2 |
| 3 |
| OA |
| 1 |
| 3 |
| OB |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
函数y=
(a>1)的图象的大致形状是( )
| |x| |
| xax |
A、 |
B、 |
C、 |
D、 |
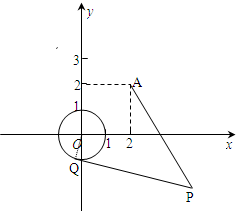 如图,已知⊙O:x2+y2=1和定点A(2,2),由⊙O外一点P(a,b)向⊙O引切线PQ,Q为切点,且满足|PQ|=|PA|.
如图,已知⊙O:x2+y2=1和定点A(2,2),由⊙O外一点P(a,b)向⊙O引切线PQ,Q为切点,且满足|PQ|=|PA|.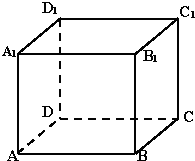 在正方体ABCD-A1B1C1D1中,棱长为a,M、N分别是A1B和AC的中点.
在正方体ABCD-A1B1C1D1中,棱长为a,M、N分别是A1B和AC的中点.